1

While studying Physical chemistry of interfaces, from: Page 42 (chapter 3 , section on "equilibrium conditions") in Butt, H. J., Graf, K., & Kappl, M. (2013). Physics and chemistry of interfaces. John Wiley & Sons. I encountered the following "theorem" from differential geometry:

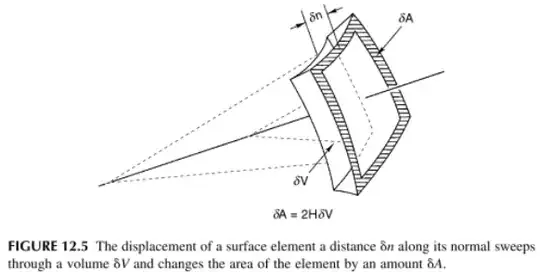
$$\frac{\partial V}{\partial A} =\left( 1/R_1 + 1/R_2 \right)^{-1} $$ where $V,A$ are the body volume and surface area, respectively, and $R_i$ are the principal radii of curvature (implying that the RHS is the inverse of the mean curvature).

Unfortunately, I couldn't find any place mentioning this statement. In addition, as emphasized in this math stack exchange post by Ted Shifrin, the radii of curvature vary from point to point, but $V$ and $A$ are global.

Will someone help me understand why this theorem is true? References might be helpful too. Are there any ways proving this statement without using fancy tools from differential geometry, but rather only multivariable calculus notions?

Thank you

The context: when trying to derive Young-Laplace equation from thermodynamics principles, $\frac{dF}{dA}=\frac{∂F}{∂A}+\frac{∂F}{∂V}\frac{∂V}{∂A}$. Then, plugging in $\frac{∂F}{∂A}=\gamma$ and $\frac{\partial V}{\partial A}=(1/R_1+1/R_2)^{−1}$ yields Young-Laplace theorem (F is Helmholtz free energy).

Dr. John
  • 197

1 Answers1

2

(For anyone trying to find the book, the actual title is Physics and Chemistry of Interfaces.)

The equation appears to refer to the swept volume and area of a differential element (figure from Dehoff, Thermodynamics in Materials Science):

enter image description here

Assume that the element is created by rotating through infinitesimal arcs $d\phi_1$ and $d\phi_2$ with respective radii of curvature $R_1$ and $R_2$. The swept volume is thus $$\delta V=R_1R_2\,\delta n\,d\phi_1\,d\phi_2.$$ The change in area when sweeping to the new radii of curvature $R_1+\delta n$ and $R_2+\delta n$ is \begin{align}\delta A&=(R_1+\delta n)d\phi_1(R_2+\delta n)d\phi_2-(R_1\,d\phi_1)(R_2\,\phi_2).\\ &\approx[R_1R_2+(R_1+R_2)\delta n]\,d\phi_1\,d\phi_2-R_1R_2d\phi_1d\phi_2\\ &=(R_1+R_2)\delta n\,d\phi_1\,d\phi_2.\end{align}

Thus, $$\frac{dV}{dA}=\frac{R_1R_2}{R_1+R_2}=\left(\frac{1}{R_1}+\frac{1}{R_2}\right)^{-1}.$$ Make sense?

Chemomechanics
  • 30,163