This questions is a follow up to a pervious question of mine:
Now that I know that Haldane phase is it's own inverse, I am having trouble is visualizing how could we stack two Haldane chains in order to get back the trivial chain. It might not be possible to have a "visual proof" at all. But, by any chance, can we employ the same construction, as used by Max Metlinski for Kitaev chain, in his Lecutre 2 about Anomalies and TQFT ( at 10:45 ).
https://youtu.be/lToc4t_Nxjc?t=646
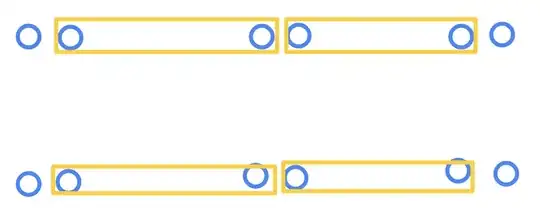
EDIT1: I will try to imitate the drawings made by Max Metlinski here. We start with two Kitaev chains. One above, and one below. Two closeby blue circle represent majorana fermions. So the two chains are in "non-trivial" phase since the fermions from two adjacent sites are paired. On each chain, there are two unpaired edge majoranas.
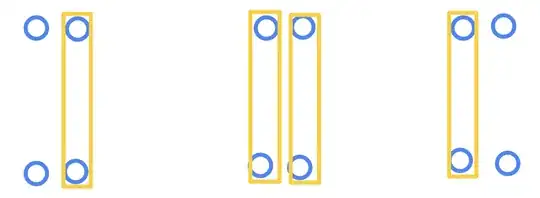
Then he asks to focus on individual boxes, and switch from horizontal links to vertical links. This is what he draws:
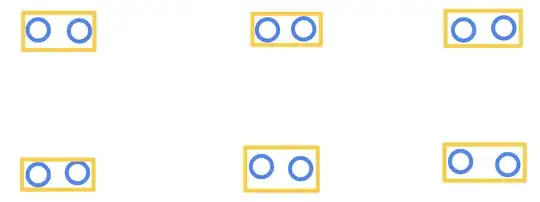
And then he asks to "rotate/flick/tilt" these so that the closest sites are linked now. I am not sure what to draw because I didn't understand this step. However, I know that ultimately, we are supposed to obtain this final configuration ( i.e. two "trivial" Kitaev chains without any edge Majorana ).
So, just to reiterate my question:
- What was the last step that he performed?
- Why would that step be unidirectional? I mean, we should not be able to combine two trivial chains to get a non-trivial chain, right ? ( We can't add the identity elements of group to get a non-identity element ).