A question regarding pressure in a moving liquid

Question

Consider a steady, streamline flow with no friction.There is a horizontal pipe and a pump is attached to one of its ends and water is pumped.The area of cross section of the pipe is uniform.So according to equation of continuity the velocity at each area of cross section must be same.My question is since there is a pressure being applied and pressure is force per unit area shouldn't the force exerted on the water by the pump make it flow with increasing velocity and not constant velocity?There must be an acceleration of the fluid in the pipe every second, right?I want an explanation at the 11th grade level.

Answer 1

You are correct that the continuity equation implies that $v$ is constant in a constant diameter pipe. Continuity comes from assuming an incompressible fluid.

If the pipe is level, the fluid passing through it is ideal (having no viscosity), and the flow is laminar (without turbulence), then the pressure in the fluid must be the same at both ends. This is a result of Bernoulli's equation $$ p + \rho g y + \frac{1}{2} \rho v^2 = \mathrm{constant}.$$ If $y$ and $v$ are the same at both ends of the pipe, $p$ is too. This is related to conservation of energy in the fluid.

If there is a pressure difference between the ends, then the fluid at the high pressure end should be slower than the fluid at the low pressure end. The fluid speeds up as it passes through the pipe. But this violates the continuity equation. (For this to work out the fluid must be compressible.)

In a real fluid viscosity supplies a friction-like force. In the horizontal pipe with no pressure difference between the ends, a real fluid would lose energy due to its viscosity. The fluid would slow down as it travels, again violating the continuity equation.

The Hagen-Poiseuille equation says that in order to maintain a steady volumetric rate of flow in a real fluid through a cylindrical pipe there must be a pressure difference between the ends of the pipe $$ \Delta p = \frac{8\pi \mu L Q}{A^2},$$ where $L$ is the length and $A$ is the cross sectional area of the pipe, $Q$ is the volumetric rate of flow, and $\mu$ is the dynamic viscosity of the fluid. This pressure difference supplies the energy that is lost to viscosity, so the speed of the fluid is the same at both ends of the pipe.

Answer 2

My question is since there is a pressure being applied and pressure is force per unit area shouldn't the force exerted on the water by the pump make it flow with increasing velocity and not constant velocity?

You have re-discovered the Bernoulli's prinicple. Well done!

Indeed, the fluid velocity changes due to the pressure (or height) difference which in the context of Newton laws of motion translates to net force on the fluid element. The Bernoulli's equation for an ideal, incompressible fluid is

$$p + \rho g y + \frac{1}{2} \rho v^2 = \text{const.}$$

Please note that fluid dynamics is much more complicated than this simple equation above due to other effects such as viscosity etc. However, the Bernoulli's equation can often be used as an excellent approximation for many practical problems.

---

Derivation of Bernoulli's equation

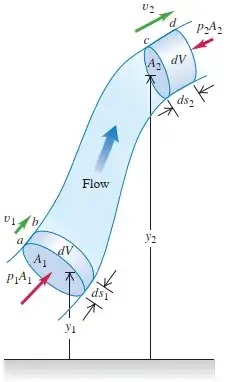
Here I give simple derivation of the Bernoulli's equation. See figure below for reference.

^{Source: H. D. Young, R. A. Freedman, "University Physics with Modern Physics in SI Units", 15th ed., 2019.}

We will apply the work-energy theorem, which states that change in kinetic energy equals work done $\Delta K = W$. Note that $d$ just denotes very small quantities - it is part of calculus which you will probably learn in later grades.

The work is defined as force times displacement $dW = F \cdot ds$. The net work on the fluid element in the figure above is

$$dW = F_1 \cdot ds_1 - F_2 \cdot ds_2 = p_1 A_1 \cdot ds_1 - p_2 A_2 \cdot ds_2 = p_1 dV_1 - p_2 dV_2 \tag 1$$

The kinetic energy difference between the two points is

$$dK = \frac{1}{2} (dm_2) v_2^2 - \frac{1}{2} (dm_1) v_1^2 = \frac{1}{2} (\rho \cdot dV_2) v_2^2 - \frac{1}{2} (\rho \cdot dV_1) v_1^2 \tag 2$$

The gravitational potential energy difference between the two points is

$$dU = (dm_2) g y_2 - (dm_1) g y_1 = (\rho \cdot dV_2) g y_2 - (\rho \cdot dV_1) \cdot g y_1 \tag 3$$

By continuity principle, since fluid (mass or volume) is not being stored in the tube, the two (infinitesimally small) volumes $dV_1$ and $dV_2$ are equal, i.e. $dV_1 = dV_2 \equiv dV$. From the work-energy theorem $dW = dK + dU$ and by combining Eqs. (1)-(3) we get

$$(p_1 - p_2) dV = \frac{1}{2} \rho \cdot dV (v_2^2 - v_1^2) + \rho \cdot dV \cdot g (y_2 - y_1)$$

which gives the final form of the Bernoulli's equation

$$\boxed{p_1 + \rho g y_1 + \frac{1}{2} \rho v_1^2 = p_2 + \rho g y_2 + \frac{1}{2} \rho v_2^2}$$

Answer 3

There is always friction; for a low friction pipe the flow rate will increase until the friction effect is sufficient for the flow to be steady. You cannot have steady flow for your case without friction.

Your situation is: steady flow, horizontal pipe of constant cross section, for an essentially incompressible liquid. Your system is the pipe. The mass flow rate is $\rho Av$ where $\rho$ is density, $A$ is flow area, and $v$ is liquid velocity. For steady flow, the mass flow rate is constant, and for your case with constant $\rho$ and constant $A$, $v$ is also constant. There is no acceleration of the liquid for steady flow. But, there is loss of pressure along the pipe due to fluid friction. To include the effect of friction, a loss term must be included in the Bernoulli equation, and the equation is then called the modified Bernoulli equation. If your system also includes a pump, a term for the work done by the pump is also included in the modified Bernoulli equation.

For an example where both pump work and friction loss are addressed, please see my answer to Power of water pump on this exchange, where I show how to determine the flow rate from a centrifugal pump in a flow network, using the modified Bernoulli equation. I can provide more details if you wish. You can find discussions of the modified Bernoulli equation online.