1

When using the method of Lagrange undetermined multipliers, it's assumed that the constraint generalized force, $Q_j$, is given by:

$$Q_j=\lambda \cdot \frac{\partial f}{\partial q_{j}}$$

Where $f$ is my constraint equation.

Why is that? I understand that it has to be somehow related to $f$, but why its derivative multiplied by a constant? Is there an intuitive reason for that?

Pedro Nogueira
  • 51

2 Answers2

0

lets look at this pendulum example, from the free body diagram you obtain :

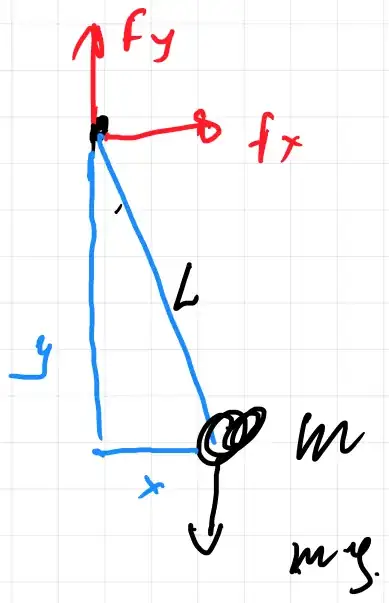
enter image description here

the EOM's with Newton second law

$$m\,\ddot x-F_x=0\\ m\,\ddot y+m\,g-F_y=0$$

where $~F_x~,F_y~$ are the constraint forces at the pivot.

additional you have the constraint equation

$$f(x,y)=x^2+y^2-L^2=0$$

if you apply the EL with the kinetic energy

$$T=\frac m2\,(\dot x^2+\dot y^2)$$

and the potential energy

$$U=-m\,g\,y+\lambda\,(x^2+y^2-L^2) $$

you obtain the EOM's

$$m\,\ddot x-\lambda\,2\,x=0\\ m\,\ddot y-\lambda\,2\,y=0$$

hence

$$F_x=\lambda\,2\,x=\lambda\frac{\partial f(x,y)}{\partial x}\\ F_y=\lambda\,2\,y=\lambda\frac{\partial f(x,y)}{\partial y}$$

or with $~Q_1=F_x~,Q_2=F_y~,q_1=x,q_2=y$

$$Q_j=\lambda\,\frac{\partial f}{q_j}$$

notice that unit of $~Q_j~$ is [N], so the unit of $~\lambda~$ in this case is $~[N/m]$

Eli
  • 13,829
0

  1. Given a holonomic constraint $$f(q,t)~\approx ~0,$$ if the Lagrangian is of the form $$L~=~T-U+\lambda f,$$ then the Euler-Lagrange (EL) equations $$0~\approx~\frac{d}{dt}\frac{\partial L}{\partial\dot{q}^j}-\frac{\partial L}{\partial q^j} ~=~\dot{p}_j-\underbrace{Q_j^{\rm cons}}_{\begin{matrix}\text{generalized}\cr\text{conservative}\cr\text{forces}\end{matrix}}- \underbrace{\lambda\frac{\partial f}{\partial q^j}}_{\begin{matrix}\text{generalized}\cr \text{constraint}\cr\text{forces}\end{matrix}} $$ becomes Newton's 2nd law. This essentially answers OP's question.

  2. This can be generalized to semi-holonomic constraints, cf. e.g. this Phys.SE post.

Qmechanic
  • 220,844