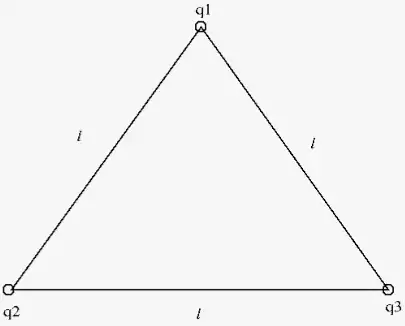
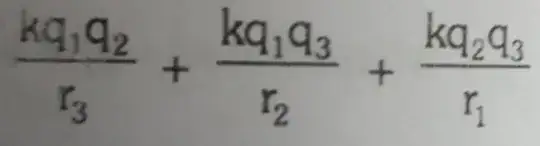Building up the distribution:
The work required to bring $Q_{2}$ in the presence of $Q_{1}$
$ \frac{Q_{2}Q_{1}}{4\pi\epsilon_{0}R_{1,2}}$
Where $R_{1,2}$ is the distance between charges 1 and 2
The work required to bring $Q_{3}$ in the presence of fields generated by $Q_{2}$ and $Q_{1}$ from infinity to its location, would be:
$\int -(\vec{F_{1}} + \vec{F_{2}}) \cdot \vec{dl}$
$\int -\vec{F_{1}} \cdot \vec{dl_{1}} + -\int\vec{F_{2}} \cdot \vec{dl_{2}}$
$\int -\frac{Q_{3}Q_{1}}{4\pi\epsilon_{0}r_{1}^2}\hat r_{1} \cdot \vec{dl_{1}} + \int -\frac{Q_{3}Q_{2}}{4\pi\epsilon_{0}r_{2}^2}\hat r_{2} \cdot \vec{dl_{2}}$
Note the path $\vec{l_{2}}$ and $\vec{l_{2}}$ are the same path, but are both defined in terms of the radial distance from each charge since we are working with 2 different variables$(r_{1},r_{2})$, so we need to define 2 different parametizations in order to integrate.
Since we are evaluating the field for each charge as a function of radial distance, the line element in spherical coordinates would be:
$\vec{dl_{1}} = dr_{1} \hat r_{1} + r_{1} d\theta_{1} \hat \theta_{1} + r_{1} sin(\theta_{1}) d\phi_{1}\hat \phi_{1}$
$\vec{dl_{2}} = dr_{2} \hat r_{2} + r_{2} d\theta_{2} \hat \theta_{2} + r_{2} sin(\theta_{2}) d\phi_{2}\hat \phi_{2}$
Since the force from each charge only has a $\hat r_{1.2}$ component, the dot product of each path with its respective force leaves only the the first component of each path. ( as the rest dissapear)
Which gives us
$\int -\frac{Q_{3}Q_{1}}{4\pi\epsilon_{0}r_{1}^2} dr_{1} + \int -\frac{Q_{3}Q_{2}}{4\pi\epsilon_{0}r_{2}^2} dr_{2}$
What are the bounds for each respective integral? Well the path that we want is a path from infinity to the location of the charge. The variables as we have it, are in terms of radial distance from each charge( as the other components vanish in the dot product) so the bounds are:
$r_{1}:$ $\infty$ to $R_{1}$, where $R_{1}$ is the final radial distance from $Q_{1}$
$r_{2}:$ $\infty$ to $R_{2}$, where $R_{2}$ is the final radial distance from $Q_{2}$
$\int_{\infty}^{R_{1}} -\frac{Q_{3}Q_{1}}{4\pi\epsilon_{0}r_{1}^2} dr_{1} + \int_{\infty}^{R_{2}} -\frac{Q_{3}Q_{2}}{4\pi\epsilon_{0}r_{2}^2} dr_{2}$
$ \frac{Q_{3}Q_{1}}{4\pi\epsilon_{0}R_{1}} +\frac{Q_{3}Q_{2}}{4\pi\epsilon_{0}R_{2}}$
Adding the total amount of work gets us
$\frac{Q_{2}Q_{1}}{4\pi\epsilon_{0}R_{1,2}} + \frac{Q_{3}Q_{1}}{4\pi\epsilon_{0}R_{1}} +\frac{Q_{3}Q_{2}}{4\pi\epsilon_{0}R_{2}}$