What physical state of a wound string corresponds to a 'tuned' string?

Question

Many instruments can be strung with strings comprised of a solid core and wound with another metal wire, e.g. the viola. I was wondering about the physical state of wound strings when they are 'in tune'. My thought was this could be when the wires are just touching one another, but I don't know if being tuned actually corresponds to an identifiable physical configuration of coils. I haven't been able to find any answer or explanation as to what the string actually looks like up close when it's in tune. I am familiar with the correlation between the string mass/length ratio and note of the string, but still do not understand why companies (such as the one above) sell distinct strings when the same notes could be achieved with the same string tuned to different tensions.
I became curious about the answer to this question over the course of solving a physics string tuning problem for designing a string tuner.

Answer 1

I am addressing this part of the question

why companies (such as the one above) sell distinct strings when the same notes could be achieved with the same string tuned to different tensions.

Consider the following table, in which we have listed the frequencies of the notes played by a guitar in standard tuning, the corresponding wavelength of the fundamental (longest-wavelength) mode on the string (which are all the same because the length of the string is the same), the wave speed $v$ on the string (as computed by multiplying the frequencies by the wavelengths), the linear mass densities $\mu$ of each string (roughly), and the finally the tensions $T$ of each string as computed using $$ v= \sqrt{T/\mu}. $$ What we observe is that the tensions are all roughly equal! As far as designing a guitar goes, this is an important choice to make, because we don't want the strings to pull on the guitar differentially, which can cause warping. This is likely the primary reason the strings are chosen to be different thicknesses.

	E2	A2	D3	G3	B3	E4
Frequency (Hz)	82.41	110	146.93	196	246.94	329.63
Wavelength (m)	1.32	1.32	1.32	1.32	1.32	1.32
Wave speed (m/s)	108.8	145.2	193.8	258.7	326.0	435.1
Density (kg/m)	0.00739	0.004366	0.002333	0.001340	0.000808	0.000481
Tension (N)	87.4	92.0	87.6	89.7	85.9	91.0

After that, the designer needs to be find way to make the strings of varying thicknesses. As pointed out by Michael Seifert in a comment below, the wires are coiled to achieve the differing thicknesses For the following reason:

"...the reason that wire-wrapped strings are used is that they are much less stiff than a solid piece of wire (or nylon or whatever) of the same mass density. For thicker wires, the resistance to bending can be sufficient to affect the harmonics of the string."

(I don't really understand the other question in the post (basically the title) because I'm not sure what you're getting at. Tuning doesn't change the configuration of the coils. All we're doing when tuning is changing the tension in the string and thereby changing the wave speed and hence the fundamental frequency on the string.)

Answer 2

Being in tune or not is a relationship of the different fundamental frequencies of your strings... It has some noticeable effects, pro acoustic guitar players for example sometimes say that they can feel whether their guitars are out of tune in the vibration of the guitar itself against their chest as they play. More notably, beat frequencies as you are close to in-tune but not quite there, are one way people actually tune their guitars etc. But the point is that the string doesn't care. The string cannot control, for instance, just how long it is going to be stretched out for, except that it'll be less than its total length. Some viola-maker decided on that length, the string-maker just needs to sell you strings long enough to tolerate a large range of typical lengths for that instrument’s size.

Now you ask why these strings are of varying thickness when one string could work at vastly different tensions. Some points:

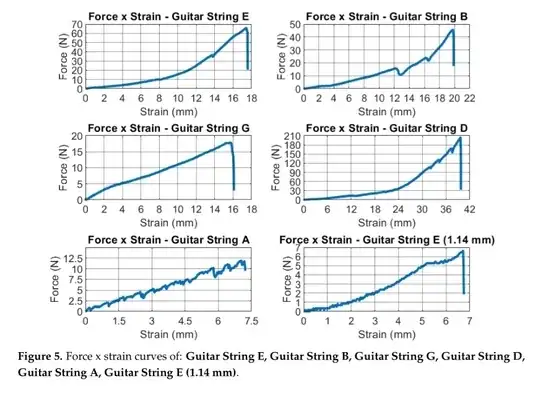
Real materials are not just ideal springs, they have what we call stress-strain curves. Here's some examples of stretching guitar strings by a fixed length and seeing what a force gauge says is the tension:

Notice first that the graphs abruptly drop on the right—the strings break, so the force gauge drops to zero. On the B string you see internal damage in the middle without the whole string breaking, as these sudden drops where stretching the string out further actually decreases the tension (because the structure inside started sliding around somehow, permanently deforming in order to handle these forces). The straight line through zero $y=mx$ behavior is what is described by Hooke's law, these all have significant deviations even as the string is stretched by maybe a percent or two. (It is not completely clear from the paper, but I believe the reference length is 25.5 cm? These graphs show nonlinearities even after a few mm at those lengths.)

Then they break, in some cases with tensions as low as 7 N. And even if it doesn't snap outright, none of these curves is straight and Hookean after that point. (Side note, those tensions are very low, other sources I've seen quote typical tensions of like 50 Newtons or so on a string in a guitar.)

Anyway my first point is just to say, if you need a frequency twice as high I think that requires a tension four times as high, and it's not totally easier that you can get to the next octave that way without snapping the string.

But even if you could, it would not be comfortable for the player. Remember, someone has to fret this! Their delicate fingers are going to be pressing down on this wire, pressing it into their instrument to achieve a certain pitch, and any increase in the tension is going to make it harder for them to push down on it. For that reason alone you want all of the different strings to have about the same tension, so that they're all about equally as difficult to press down. Quadrupling the tension over here will mean that this string takes four times more effort to push down than that other string, and that's just not a very uniform experience for the player.

Other than those two issues, you do have to consider that the tension in the strings actively pulls the beam forward, and often has to be resisted by some sort of tensioning rod. So the convention of how much tension is in those strings is something that you would not want to stray too far from, since it means that to restring your guitar you also need to adjust the tension in the fretboard etc.

(Figure 5 above came from “Evaluation of Commercial Ropes Applied as Artifi cial Tendons in Robotic Rehabilitation Orthoses” by Rúbio et al.)

Answer 3

For a string to be in tune is in no way distinctive from a physical standpoint. Musical pitches are just a convention, the corresponding frequencies even change with culture and era.

However it is not practical to tune a fat string very high (tension would break it), or to tune a thin string too low (string would end up quite loose producing hardly any sound).