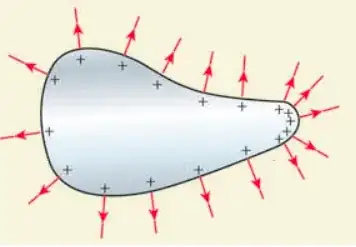
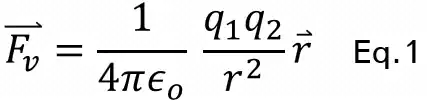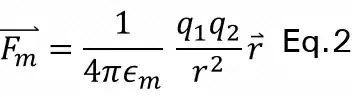charges accumulate on sharp edges more than flat edges.
3 Answers
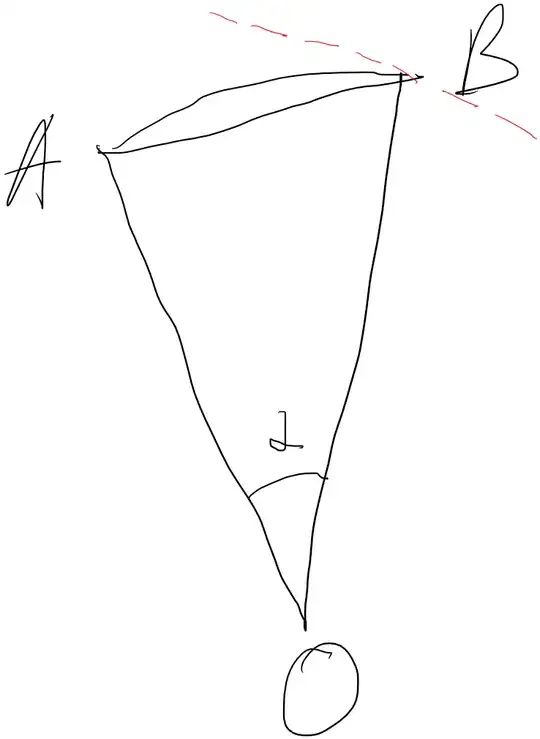
Like charges on the surface of a conductor repel each other. Let us consider two identical charges $q$ in points A and B on the surface of a conductor in an area where the curvature of the surface is $R$, so OA=OB=R (see the picture). Let us assume that the length of arc AB is $l$, and $l\ll R$. Then angle $\alpha=l/R$. The distance between the charges AB=$\delta=R\cdot2\sin\frac{\alpha}{2}$. The Coulomb force between the charges is directed along AB, and its magnitude is $\frac{q^2}{\delta^2}$. However, the normal component of the Coulomb force cannot move the charges, so we need to calculate the tangential component of the Coulomb force. The angle between AB and the red dashed tangent to the curve is $\frac{\alpha}{2}$, so the tangential projection of the Coulomb force is $$\frac{q^2}{\delta^2}\cos\frac{\alpha}{2}=\frac{q^2}{R^2\cdot 4\sin^2\frac{\alpha}{2}}\cos\frac{\alpha}{2}=\frac{q^2}{\frac{l^2}{4 x^2}\cdot 4\sin^2 x}\cos x=\frac{q^2}{l^2}\frac{x^2\cos x}{\sin^2 x},$$ where $x=\frac{l}{2 R}\ll 1$.
Let us use the following approximation: $$\frac{x^2\cos x}{\sin^2 x}\approx \frac{x^2(1-\frac{x^2}{2})}{(x-\frac{x^3}{6})^2}\approx\frac{x^2(1-\frac{x^2}{2})}{x^2-\frac{x^4}{3}}=\frac{1-\frac{x^2}{2}}{1-\frac{x^2}{3}}\approx(1-\frac{x^2}{2})(1+\frac{x^2}{3})\approx$$ $$\approx 1-\frac{x^2}{6}. $$Thus, if the arc length $l$ is constant and the radius of curvature decreases, $x$ increases, and the tangential component of the Coulomb force between the charges decreases. Therefore, one can expect that the charge density will be greater in the areas where the curvature is greater.
- 27,962
In an electrostatic situation the voltage on the surface of a conductor has to remain constant, however when the surface changes rapidly in space such as in the case of a sharp edge or a spike the voltage function also has to change rapidly to compensate. A rapidly changing voltage $V$ will mean a very high surface charge density $\sigma$ since $$\sigma = -\epsilon_0 \frac{\partial V}{\partial n}$$where $\partial/\partial n$ is the surface derivative.
- 1,913
If we have two charges Q1 and Q2 separated by a distance r in a vacuum. the force between them is given by equation #1.
Where ϵ_o is the permittivity of vacuum.
If we put the charges in another medium, the force between the two charges is given by equation #2
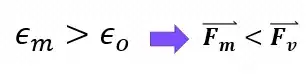
the force between the two charges will be decreased since the permittivity of any medium is larger than the permittivity of vacuum.
If we put the two charges on the surface of a metallic conductor which has an irregular shape the force between the two charges depends on whether the surface is flat or curved.
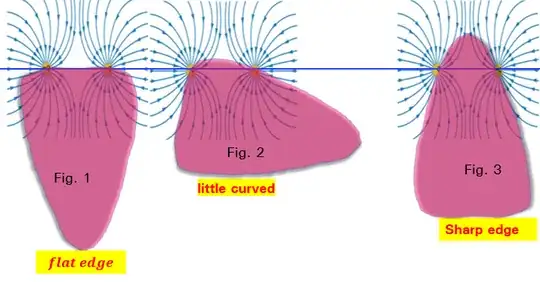
Assume we put the two charges at the same distance on fig1, fig2, and fig 3.
If the surface is flat as we see in fig. 1 the conductor shield almost half the electric field lines which means the force between the two charges approximately equals half its value in a vacuum.
In fig.2 the surface gets a little curved and shields more electric field lines than in fig. 1, which means the force between the two charges is less than in the case of fig. 1.
In fig.3 the surface of the conductor gets sharper and shields more electric field lines than in fig2 and fig1, and the force between the two charges decreases more than in the Case of fig.2.
The charges leave the flat edges which have the higher repulsive force and accumulated at sharp edges where the force between them is minimum.
In conclusion as much the surface gets curved the electric field lines get shielded more and more, which means the force between the two charges at sharp edges is less than the flat edge.
So, if we charge a metallic conductor that has an irregular Shape the charges density will be large on sharp edges than on flat ones. We should also mention that a large charge density at sharp edges means a large electric field.