1

Given the 2D coordinates of two points, $a$ and $b$, between which an elastic cable of known length, $l$, mass per unit length, $m$, and the spring constant, $e$, is slung, I need to compute the shape of the cable, and also the horizontal tension, $t$, in the cable.

So far I have the equations for the x and y coordinates of the cable, parameterized by $p$, which is the distance along the unstretched cable: $$ f_x(p) = \frac{t}{mg} \sinh^{-1}\left(\frac{mgp}{t}\right) + \frac{tp}{e} + c_x.\\ f_y(p) = \sqrt{\left(\frac{t}{mg}\right)^2 + p^2} + \frac{mgp^2}{2e} + c_y.\\ $$ where $c_x$ and $c_y$ are constants, which leads me to the following triplet of simultaneous equations: $$ f_x(q) - f_x(r) = a_x - b_x.\\ f_y(q) - f_y(r) = a_y - b_y.\\ |q-r| = l. $$ in three unknowns, $t$, $q$ and $r$ (given that the constants cancel), where $q$ and $r$ are the values of the parameter $p$ at the points $a$ and $b$ respectively.

How would you compute those unknowns, and can it be done in closed form?

Qmechanic
  • 220,844
user664303
  • 111

2 Answers2

2

The shape is still a catenary regardless of the degree of elasticity of the cable.

Put a coordinate system on the left support and note the relative coordinates of the right support as $\pmatrix{S & h}$

The equation of the catenary is $$ y(x) = y_C + a \left( \cosh \left( \frac{x-x_C}{a} \right) -1 \right) $$

where $\pmatrix{x_C & y_C}$ is the lowest point on the curve, and $a=\frac{H}{w}$ is the catenary constant, derived from the horizontal tension $H$ and the unit weight $w$ (in force/length units).

To find the curve through the points $\pmatrix{0&0}$ and $\pmatrix{S&h}$ use the following coordinates for the lower point

$$\begin{align} x_C & = \frac{S}{2} - a \,\sinh^{-1} \left( \frac{ \frac{h}{a} {\rm e}^{\frac{S}{2 a}} }{ {\rm e}^{\frac{S}{a}}-1 } \right) \\ y_C & = a \left( 1 - \cosh \left( \frac{x_C}{a} \right) \right) \end{align} $$

Once the shape is known the rest of the properties can be evaluated

$$ \begin{cases} T(x) = H \cosh \left( \frac{x-x_C}{a} \right) & \mbox{Tangential Tension} \\ V(x) = H \sinh \left( \frac{x-x_C}{a} \right) & \mbox{Vertical Tension} \\ L(x) = a \sinh \left( \frac{x-x_C}{a} \right) & \mbox{Length of Cable from Lowest Point} \\ D(x) = \frac{x h}{S} - y(x) & \mbox{Cable Sag from ideal line} \end{cases}$$

So for example the total length of the cable between supports is

$$ L = L(S) - L(0) = a \left( \sinh\left( \tfrac{x_C}{a}\right) + \sinh \left( \tfrac{S-x_C}{a} \right) \right) $$

Additionally, the average tension on the cable is found by the integral

$$ P = \tfrac{1}{L} \int \limits_0^S T(x) \sqrt{ 1 + \left( \tfrac{{\rm d}}{{\rm d}x} y(x) \right)^2 } {\rm d}x = \tfrac{S w}{2} \frac{1+\tfrac{a}{2 S} \left( \sinh\left( \tfrac{2x_C}{a}\right) + \sinh\left(\tfrac{2(S-x_C)}{a}\right)\right)}{\sinh\left( \tfrac{x_C}{a}\right) + \sinh\left( \tfrac{S-x_C}{a}\right)} $$

For an even span, the above average tension is approximated well with $$ P = \frac{2 H + T}{3}$$

Now if the horizontal tension is to be calculated from a) Sag, b) Average Tension or c) Total Length then a numerical method is needed.

For example if the maximum sag $D_{\rm set}$ is known, then start with an initial guess of $H_{\rm init} = \tfrac{w \sqrt{S}}{8\,D_{\rm set}}$ and iterate finding $x_C$, and then $D$ and adjusting the tension accordingly until $|D-D_{\rm set}| < {\rm tolerance}$. If you need more details, I propose you ask a new question that references this question.

Below is a screenshot of a catenary shape solver I developed for fun using the above equations.

scr

References:

  1. https://physics.stackexchange.com/a/304484/392
  2. https://physics.stackexchange.com/a/101787/392
John Alexiou
  • 40,139
0

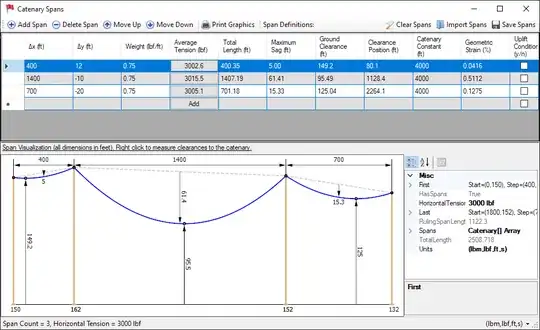
I don't know about a closed form solution, but I use the Gauss-Newton optimization approach to solve the problem, in fewer than 20 iterations usually, using the C code below. 

#include <cmath>

/* Automatically generated functions to compute residuals and Jacobian of residuals */
inline void compute_residuals(const double data[5], const double params[2], double res[2])
{
    double t2, t3, t4, t5, t6, t7, t8, t9;
    t2 = 1.0/data[3];
    t3 = 1.0/params[0];
    t4 = params[1]+data[2];
    t5 = params[0]*params[0];
    t6 = 1.0/(data[3]*data[3]);
    t7 = t5*t6;
    t8 = params[1]*params[1];
    t9 = t4*t4;
    res[0] = -data[0]+t2*params[0]*log(sqrt((t3*t3)*(t4*t4)*(data[3]*data[3])+1.0)+t3*t4*data[3])-t2*params[0]*log(sqrt((t3*t3)*(params[1]*params[1])*(data[3]*data[3])+1.0)+t3*params[1]*data[3])+t4*params[0]*data[4]-params[0]*params[1]*data[4];
    res[1] = -data[1]-sqrt(t7+t8)+sqrt(t7+t9)-t8*data[3]*data[4]*(1.0/2.0)+t9*data[3]*data[4]*(1.0/2.0);
}
inline void compute_jacobian(const double data[5], const double params[2], double J[4])
{
    double t2, t3, t4, t5, t6, t7, t8, t9, t10, t11, t12, t13, t14, t15, t16, t17, t18, t19, t20, t21, t22, t23, t24;
    t2 = params[1]+data[2];
    t3 = 1.0/(params[0]*params[0]);
    t4 = data[3]*data[3];
    t5 = 1.0/data[3];
    t6 = 1.0/params[0];
    t7 = params[0]*params[0];
    t8 = 1.0/(data[3]*data[3]);
    t9 = t2*t2;
    t10 = t7*t8;
    t11 = params[1]*params[1];
    t12 = t3*t4*t9;
    t13 = t12+1.0;
    t14 = 1.0/sqrt(t13);
    t15 = t3*t4*t11;
    t16 = t15+1.0;
    t17 = 1.0/sqrt(t16);
    t18 = t10+t11;
    t19 = 1.0/sqrt(t18);
    t20 = t9+t10;
    t21 = 1.0/sqrt(t20);
    t22 = params[1]*2.0;
    t23 = data[2]*2.0;
    t24 = t22+t23;
    J[0] = -t2*t14+t17*params[1]+t5*params[0]*log(sqrt((t2*t2)*(t6*t6)*(data[3]*data[3])+1.0)+t2*t6*data[3])-t5*params[0]*log(sqrt((t6*t6)*(params[1]*params[1])*(data[3]*data[3])+1.0)+t6*params[1]*data[3])+t2*params[0]*data[4]-params[0]*params[1]*data[4];
    J[1] = -t7*t8*t19+t7*t8*t21;
    J[2] = t14-t17;
    J[3] = t21*t24*(1.0/2.0)-t19*params[1]+t24*data[3]*data[4]*(1.0/2.0)-params[1]*data[3]*data[4];
}

/* Update the parameters with an iteration of Gauss-Newton, and return the score of the starting position */
inline double gauss_newton_iteration(const double data[5], double params[2])
{
    /* Compute the residuals and Jacobian of resdiduals */
    double score, res[2], J[4], H[3], det;
    compute_residuals(data, params, res);
    compute_jacobian(data, params, J);

    /* Compute the score, inverse Hessian and Jacobian of the cost function */
    score = res[0] * res[0] + res[1] * res[1];
    H[2] = J[0] * J[0] + J[1] * J[1];
    H[1] = -(J[0] * J[2] + J[1] * J[3]);
    H[0] = J[2] * J[2] + J[3] * J[3];
    det = 1.0 / (H[0] * H[2] - H[1] * H[1]);
    H[0] *= det;
    H[1] *= det;
    H[2] *= det;
    J[0] = J[0] * res[0] + J[1] * res[1];
    J[1] = J[2] * res[0] + J[3] * res[1];

    /* Compute the parameter update */
    params[0] *= exp(-(H[0] * J[0] + H[1] * J[1]));
    params[1] -= H[1] * J[0] + H[2] * J[1];
    return score;
}

/* Given an initial Pa, compute T0 */
inline double compute_T0(const double data[5], const double Pa)
{
    double T0 = Pa + data[2];
    T0 = data[1] + 0.5 * data[3] * data[4] * (Pa * Pa - T0 * T0);
    T0 = (T0 + data[2]) * (T0 - data[2]) * (data[2] - T0 + 2.0 * Pa) * 0.5 / (T0 + 1e-300);
    T0 = sqrt(abs(T0));
    return T0 * data[3] + 1e-15;
}

/* Given parameters and distance along the line (0 being start, 1 being end), compute a tension */
inline double compute_tension(const double data[5], const double params[2], double P)
{
    P = params[1] + data[2] * P;
    P = sqrt(P * P * data[3] * data[3] + params[0] * params[0]);
    return P;
}

/* Given a 3D start point and end point, compute the tension at those two 
 * points of an elastic line slung between the points.
 *
 *IN:
 *   start - 3D coordinates (XYZ in metres) of the start point of the line (gravity acts in the -Z direction).
 *   end   - 3D coordinates (XYZ in metres) of the end point of the line (gravity acts in the -Z direction).
 *   l     - scalar length of line (unstretched) between the start and end points.
 *   m     - mass per unit length (in Kg/m) of the line (unstretched).
 *   e     - coefficient of elasticity of the line.
 *   Pa    - estimate of position along the line (in m, unstretched) of the start point, zero being the horizontal point of the catenary.
 *
 *OUT:
 *   T     - line tensions (in N) at start, end, and the point of zero vertical tension.
 *   return value - computed value of Pa.
 */
double elastic_catenary(const double start[3], const double end[3], const double l, const double m, const double e, const double Pa, double T[3])
{
    int iter;
    double last_score, score = 1.0e300;
    double params[2];
    double data[5] = {0, end[2]-start[2], l, m * 9.81, 1.0 / e};
    data[0] = sqrt((end[0] - start[0]) * (end[0] - start[0]) + (end[1] - start[1]) * (end[1] - start[1]));

    /* Initialize parameters */
    params[1] = Pa;
    params[0] = compute_T0(data, Pa);

    /* Do the optimization */
    for (iter = 0; iter < 100; ++iter) {
        last_score = score;
        score = gauss_newton_iteration(data, params);
        if (score <= last_score && (last_score - score) <= (last_score * 1e-10))
            break; /* Converged */
    }

    /* Compute the tensions */
    T[0] = compute_tension(data, params, 0); /* Tension at line start */
    T[1] = compute_tension(data, params, 1); /* Tension at line end */
    T[2] = params[0];                        /* Tension at the horizontal point  */

    /* Return computed value of Pa - useful for initializing future optimizations */
    return params[1];
}
user664303
  • 111