Special relativity: what can be evaluated on the basis of the Minkowski metric alone?

Question

I have edited the question:
I've come to realize that there is an ambiguity that I should have recognized, but I didn't. My edit of the question is towards removing the ambiguity. Please check the diffs.

I have been challenged by someone who is quite combative about it.

The context:
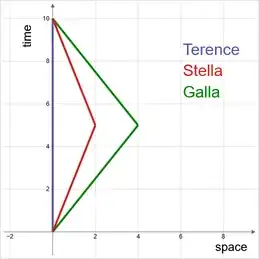
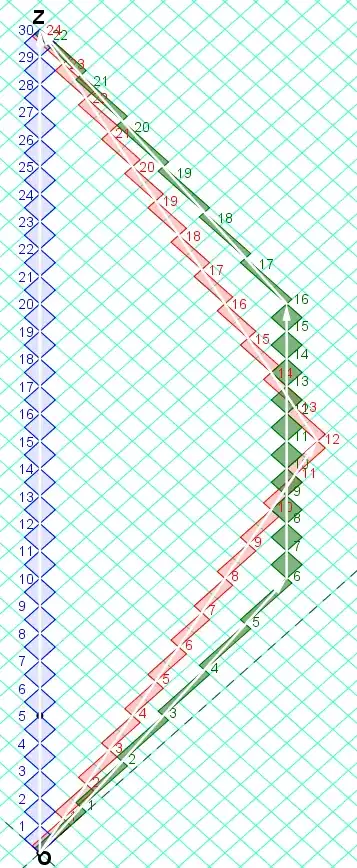
The first diagram shows the most straightforward implementation of the Twin Scenario thought experiment.

In this version there are three protagonists, I call them: Terence, Stella, and Galla. Terence stays at home, Stella goes out to the stars and Galla goes out to even more distant stars.

In this version of the twin, scenario clocks are compared at only two-point in time: before departure, and after rejoining.

The comparison will be in the form of the ratio of amount of proper time that has elapsed. Using $\tau_G$ for the amount of proper time that has elapsed for Galla, and $\tau_S$ for the amount of proper time that has elapsed for Stella the comparison will be in the form of $\tau_S/\tau_G$

The coordinate system of the diagram is the inertial coordinate system that is stationary with respect to Terence. I will refer to this as 'the global inertial coordinate system'.

(As is common practice in thought experiments: the U-turns are assumed to be taking only a negligible amount of time compared to the overall duration of the journey so it is not necessary to consider the duration of making the U-turn.)

As we know, upon rejoining it will be seen that for Stella a smaller amount of proper time has elapsed than for Terence, more so for Galla. For Galla, a smaller amount of proper time will have elapsed than for Stella.

In this version, with the clocks being compared only before departure and after rejoining, it is not necessary to consider the relativity of simultaneity effects or what have you; those effects all drop out of the evaluation.

For the motion depicted in the diagram the Minkowski metric alone is sufficient to evaluate the proceedings.

(I'm careful to not attribute causation here. Of course: in any physics taking place there must be some form of causation. However: to attribute causation to some specific feature isn't a necessity. Even while not attributing causality one can still do physics. In this context I'm limiting the consideration to establishing logical correlation.)

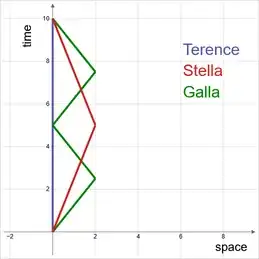
The second diagram shows a journey for Galla where she makes three U-turns instead of only one.

In the diagram 2 scenario, the amount of proper time that will be seen to have elapsed for Galla is the same as in the diagram 1 scenario.

This illustrates that in the twin scenario the amount of acceleration with respect to the global inertial coordinate system is not a factor. It is sufficient to evaluate the distance that Galla travels (with respect to the global inertial coordinate system). Galla travels more distance than Stella, and correspondingly upon rejoining of all three it will be seen that for Galla a smaller amount of proper time has elapsed than for Stella.

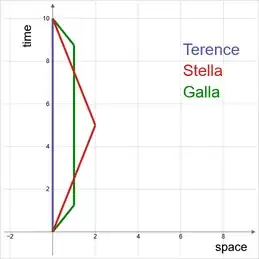
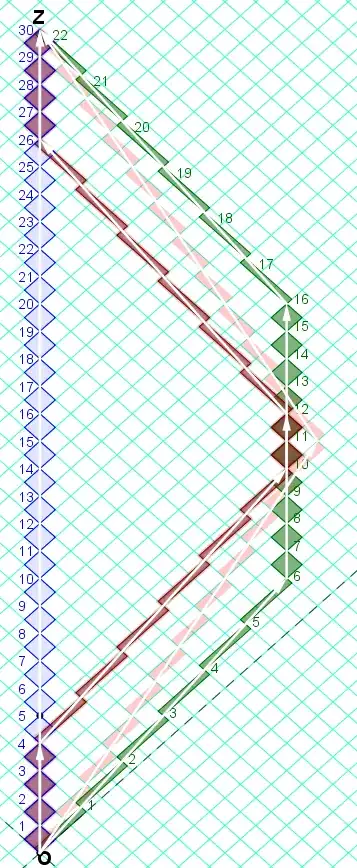
The third diagram illustrates the point where my combatant is challenging me.

In this scenario, Galla travels a smaller distance than Stella (wrt the global inertial coordinate system), but when she is moving she is moving faster than Stella ever does.

My combatant insists that the difference in the amount of proper time that elapses correlates with the Lorentz gamma factor, not with the distance traveled. Based on that my combatant argues that it is possible to have a scenario where Galla travels a shorter distance than Stella, but by traveling faster, Galla will upon rejoining be seen to have clocked up a smaller amount of proper time than Stella has.

(Now: it's hard for me to not be biased against my combatant's point of view. So I'm probably not doing a good job of representing the point of view of my combatant. So: don't take my word for it.)

Of course, I could go through the specific calculation for the scenario of diagram 3, and some other similar trajectories, but in my opinion, I shouldn't have to do that. In my opinion, the evaluation should capitalize on having a general principle: the Minkowski metric.

The journey will have subsections, in the sense that you need at least one U-turn; the only way to rejoin is to make a U-turn somewhere. Any trajectory consists of a concatenation of subsections that are each sufficiently straight for the Minkowski metric to be applied. (If necessary subdivide the trajectory into an arbitrarily large set of subsections and evaluate it by integration.)

A specific condition of this version of the sibling scenario is that Galla and Stella must reunite with Terence together. As represented in the diagram, in order to make that happen Galla has to coast for an extended duration. As stated at the start: the outcome is to be stated in terms of ratio of proper time elapsed: $\tau_S/\tau_G$. The long duration of the coasting phase will affect the value of that ratio.

We know for sure that for Terence the amount of proper time is maxed out. If the Minkowski metric holds good then for any traveler it follows geometrically that upon rejoining it will be seen that for the traveler a smaller amount of proper has elapsed than for Terence.

The specific question:
Is there any journey for Galla such that Galla traverses a shorter distance than Stella, but by traveling faster Galla manages to make the ratio of proper time elapsed, $\tau_S/\tau_G$, larger than one.

General discussion

Physics Stackexchange contributor Kevin Zhou has pointed out something about derivation in physics that in my opinion is very significant:

[...] in physics, you can often run derivations in both directions: you can use X to derive Y, and also Y to derive X. That isn't circular reasoning, because the real support for X (or Y) isn't that it can be derived from Y (or X), but that it is supported by some experimental data D.

One can start with the Lorentz transformations and derive the Minkowski metric, or one can start with the Minkowski metric and derive the Lorentz transformations.

The direction in which one proceeds through the derivation does not inform one about the direction of causality (or even whether thinking in terms of causality is at all applicable).

Answer 1

The answer is yes, in the frame of Terence it is possible for Galla to travel a shorter distance than Stella and yet still experience a shorter elapsed time.

The reason is that the distance travelled by either of the travellers increases linearly with their speed, whereas the reduction in elapsed time increases in a faster non-linear way with speed.

To take a concrete example, imagine Galla travels out and back at 0.8c and Stella at 0.1c- you will find that Stella has to travel a vastly greater distance to achieve the same overall reduction in elapsed time compared to Terence.

Answer 2

I don't understand your comment

Of course, I could go through the specific calculation for the scenario of diagram 3, and some other similar trajectories, but in my opinion, I shouldn't have to do that. In my opinion, the evaluation should capitalize on having a general principle: the Minkowski metric.

Everything in special relativity uses the Minkowski metric.
The proper-time along a worldline (whether inertial or non-inertial) uses the Minkowski-metric to compute this spacetime-arclength along the worldline.

---

My visualizations of proper-time along piecewise-inertial worldlines use the Minkowski metric. (In fact, the "light-clock diamonds" [traced out by light-signals in a standard-issue light-clock] encode the Minkowski metric. By Lorentz invariance, all light-clock diamonds have the same area.)

As I suggested in my comment, one should primarily focus on the arc-length (and not on spatial-distances, velocities, or accelerations, which may play a role in executing the various worldlines).

Here are some diagrams that I think capture some of your concerns.
I will restrict to piecewise-inertial worldlines with nice velocities (0, (3/5)c, and (4/5)) [with corresponding Doppler factors (1,2,3)] that lead to Pythagorean triples so that we can measure by counting diamonds and calculations can be expressed as fractions.

---

First, here is an example like your diagram 3, where part of Galla's worldline is parallel to Terence's.

• Galla travels with velocity (4/5)c for 3 ticks, velocity 0c for 10 ticks, then -(4/5)c for 3 more ticks, arriving at the reunion event Z having aged 16 ticks since the separation event O. (All of these times are measured by Galla's wristwatch.)
• Stella travels with smaller-magnitude velocity (3/5)c for 8 ticks, then returns at -(3/5)c for another 8 ticks. Stella also happens to age 16 ticks between separation and reunion. (All of these times are measured by Stella's wristwatch.)
• Terence (who is inertial) aged 20 ticks.

In Terence's frame, the initially-faster-outbound Galla travels less spatial-distance than initially-slower-outbound Stella.
In this scenario, however, Galla and Stella have aged the same upon reunion.

---

Next, here's a different variation of diagram 3.

• Galla travels with velocity (4/5)c for 6 ticks, velocity 0c for 10 ticks, then -(4/5)c for 6 more ticks, arriving at the NEW reunion event Z having aged 22 ticks since the separation event O.
• Stella travels with smaller-magnitude velocity (3/5)c for 12 ticks, then returns at -(3/5)c for another 12 ticks. Stella aged 24 ticks between separation and reunion.
• Terence (who is inertial) aged 30 ticks.

In Terence's frame, the faster Galla (again) travels less spatial-distance than the slower Stella.
In this scenario, however, Galla aged 22 ticks, which less than slower Stella's 24 ticks.

So, comparing with the previous case, it seems that:
the fact that "the initially-faster-outbound Galla traveled a shorter distance than the initially-slower-outbound Stella" doesn't tell us who aged more between separation and reunion.

As an alternative to Galla's worldline, we have another piecewise-inertial worldline to approximate the worldline given by @AdamHerbst.
The brown-worldline doesn't cross Stella's worldline. By counting, you can see that it traveled the same spatial-distance as Galla and that it aged the same 22 number of ticks between separation and reunion (which is less than Stella's 24 ticks).

Re-iterating my comment:
one should primarily focus on the arc-length (and not on spatial-distances, velocities, or accelerations, which may play a role in executing the various worldlines).

Answer 3

The proper time between two points in spacetime is given by $$c^2\Delta \tau^2=c^2\Delta t^2-\Delta x^2.$$ You can calculate the total proper time of any of these travels by calculating the proper time on each straight line segment and summing the results together.

So the answer to your specific question: possibly yes. You could calculate the proper time of each of these paths and compare the results. Generally speaking the closer to a straight line you are the longer the proper time.

Answer 4

Marco Ocram is exactly right, the proper time doesn't depend solely on the distance traveled. It's easy enough to calculate the exact differences in proper time relative to Terence's so here it is. Suppose Galla (or Stella, it doesn't matter) travels a distance $X$ (in Terence's coordinates) at velocity $v = \beta c$. Since the "vertical" portions of the worldlines don't contribute any difference in proper time relative to Terence's, we can focus only on the portions where Galla is in motion. The corresponding proper time for Terence is $$c\tau = \frac{2X}{\beta}$$ and for Galla it is $$c\tau = 2\sqrt{\left(\frac{X}{\beta}\right)^2 - X^2}$$ where the factors of 2 deal with the fact that the proper times along the trip to and from $X$ are equal. The difference between Terence and Galla's proper times is $$c\Delta\tau=\frac{2}{\beta}\left(1-\sqrt{1 - \beta^2}\right)X. $$ Note the velocity dependence.

Answer 5

In my opinion, the evaluation should capitalize on having a general principle: the Minkowski metric.

Oh sure, that is the second easiest way to do it!¹

What is the Minkowski metric? $$ (\Delta \tau)^2 =(\Delta t)^2 -\|\Delta \mathbf r/c\|^2.\tag1 $$

In the third diagram for Galla you are trying to split the coordinate time into two parts$$\Delta t =\Delta t_1+\Delta t_2$$ (say, $\Delta t_2=p~\Delta t,~~\Delta t_1=(1-p)\Delta t$ or so) such that each will have its own $\Delta\mathbf r_{1,2}$ and $\Delta \tau_{1,2}.$ In particular you seem interested in $\Delta\mathbf r_2=0$ hence eq (1) says $\Delta \tau_{2}=\Delta t_{2},$ then $p$ is the proportion of the coordinate time $\Delta t$ that Galla spends at rest.

On the other hand eq (1) says that $\Delta \tau_1=(1-p)\Delta t/\gamma$ can be driven arbitrarily close to 0 by choosing a velocity sufficiently close to the speed of light. We can assume it's negligible or we can just include it in the math since the math is not hard... Then assuming Stella has some relation $\Delta t=\gamma_\text{S}~\Delta \tau_\text{S},$ the goal is to find $$\Delta \tau_1+\Delta\tau_2 < \Delta\tau_\text{S},\\ \frac{(1-p)\Delta t}{\gamma_\text{G}}+p~\Delta t < \frac{\Delta t}{\gamma_\text{S}},\\$$ And removing $\Delta t$ entirely we just have$$ p < \frac{(\gamma_\text{G}/\gamma_\text{S})-1}{\gamma_\text{G}-1}.\tag2 $$ Under the very weak assumption that $\gamma_\text{G}>\gamma_\text{S},$ this number exists. With some real numbers (say $\gamma_\text{G}=3, \gamma_\text{S}=1.5$), Galla could spend 1/3 of the time flying out, 1/3 of the time at rest, and 1/3 of the time flying back in. Those speeds are 75% c and 94% c, so the distance measured is for sure lower (i.e. 94% c times 66.7% Δt is less than 75% c times 100% Δt).

More interestingly, given that you want to have Galla spend 90% of the time at rest (roughly what you drew in your diagram), eq (2) places a common sense restriction on Stella, Stella’s time cannot be too dilated because if $\gamma_\text S>10/9$ then Stella simply will experience less time than 90% Δt and Galla can't make it work while staying at rest for 90% Δt. So if we want $p=0.9$ then we need Stella at a very low $\gamma_\text{S} $ like 1.05 to match, but we then get a comparatively large $\gamma_\text{G} a\approx 2$ as we try to half-spend the remaining 10% of the time.

1. The easiest way is to recognize that once you have done the first analysis you did, some such $p$ just must exist. Set up the first analysis but halfway through Galla’s acceleration have the space ship pause at rest for one picosecond. This can't possibly change anything material, Galla must live the shortest time of the three. But this has the shape of your third situation directly.

Answer 6

Yes, it is possible. Here is an example of two paths with this property. First, let $t$ be the time coordinate in the global Terence frame, $v_S(t)$ and $v_G(t)$ be the speeds (not velocities) of Stella and Galla w.r.t this frame, and use the convention $\beta = \frac{v}{c}$. Finally, let $T$ be the duration of all paths in this frame. Then the distance traveled on any path is

$d = \int_0^T v(t)dt = c\int_0^T \beta(t)dt$

whereas the proper time according to the Minkowski metric is

$c\tau = \int_0^T \sqrt{c^2 dt^2 - dx^2} = c\int_0^T \sqrt{1 - \beta^2(t)}dt$

Now let Galla take the path defined by $\beta_G(t) = \sin\frac{\pi t}{T}$. Hence her speed is zero at the start and end, and just reaches the speed of light at the halfway point, where she turns around. Meanwhile, Stella follows $\beta_S(t) = \frac{\sqrt 2}{2}$, ie. she maintains constant speed, as in your first diagram.

Thus, $\sqrt{1 - \beta_G^2} = |\cos{\frac{\pi t}{T}}|$, while $\sqrt{1 - \beta_S^2} = \frac{\sqrt 2}{2}$.

Plugging all these expressions into the integrals above, we find

$$d_G = c\tau_G = \frac{2}{\pi} cT\\ d_S = c\tau_S = \frac{\sqrt 2}{2} cT$$

Hence, both the distance and proper time are smaller for Galla than for Stella.

This is just one example, but since both quantities differ by a finite amount ($\frac{\sqrt 2}{2} - \frac{2}{\pi}$), it would be possible to deform the paths continuously in many ways and still maintain the property you requested.

EDIT: Here is the diagram of the two paths calculated above, for $T = 1 \text s$. You can easily see that Galla (red path) travels less distance. But (qualitatively speaking) because she spends a lot of time at higher speed than Stella, her proper time is also less.