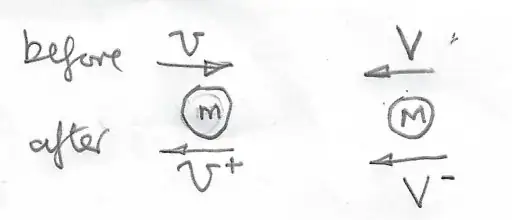What is the extra kicks to accelerate a spacecraft during gravity assist?

Question

Suppose a spacecraft coming from behind a planet during a flyby, it gets a boost in speed and also change in direction of travel but where does this extra kicks come from? Now that I understand gravity isn't exactly a true force so what is actually slingshotting the spacecraft and how come it have to change it's direction of travel? Does it matters if the spacecraft is moving at a constant speed or it has to accelerate to benefit from the gravity assist?

Answer 1

For almost all real-world purposes, treating gravity as a real force that just happens to work just like a pseudoforce is good enough.

Suppose all you have is a rocket and planet X. You want to move as fast as possible relative to planet X. Can you gravity assist to do that? No. While you are moving towards planet X, planet X's gravitational field does work on your space ship. While you are moving away from planet X, your space ship does the same amount of work back on the gravitational field. The total work done is zero, so the total change in relative speed is zero; all you've done is changed direction.

However, suppose you have a rocket, planet X, and planet Y. You want to move as fast as possible relative to planet X. Planet Y has a certain relative velocity to planet X. If you can use your rocket booster to start with a relative speed to planet Y and end with the same relative speed to planet Y, but in a different direction, your speed relative to planet X can have increased.

Gravity assists are often treated as being like elastic collisions, and an elastic collision makes an easy way to move the question into the world of practical every day effects. Suppose you have a tennis ball and a train zipping past you at 130 km/h. If you fling the tennis ball at the front of the train at 50 km/h (relative to you), its initial speed relative to the train is 180km/h and its final speed relative to the train is 180km/h in the opposite direction (less a bit since it's not a perfectly elastic collision). However, the tennis ball's initial speed relative to you was 50 km/h, and it's final speed relative to you is 310km/h (180km/h relative to the train plus the train's 130km/h relative to you). If you're trying to throw the ball as far away from the train as possible, there's no point in throwing it at the train, you could just throw it past the train and the train will go past on its own. But if you're trying to throw the ball as far away from you as possible, bouncing it off of the high speed train is a pretty good idea.

Answer 2

In general terms you are looking the elastic interaction between two masses, $m$ and $M$, approaching each other with speeds $v$ and $V$, and $M\gg m$ as shown in the diagram below.

The result of such an interaction is that the smaller mass (tennis ball) "rebounds" off the larger mass (tennis racket and player) with an increased speed $v^+ > v$ and the speed of the larger is decreased $V^+<V$.
This can be shown by using the conservation of momentum (no external forces) and conservation of kinetic energy (elastic collision).
So the smaller mass gains some kinetic energy at the expense of the larger mass.

It is perhaps easier to imagine such an interaction via a repulsive force as in the left hand diagram (hypothetically satellite "bouncing off" the planet) than via an attractive force (gravity assist).

Note that if the direction of motion of the planet is reversed then the satellite would lose some kinetic energy.

Answer 3

For the sake of the problem you are facing, treating gravity as a force it’s an idea that simplifies things, without backlashes. This said, what should bother you first and foremost, is the fact that gravity is a conservative “force”, i.e., all energy you gain from falling towards a planet from height $h$ will be lost when you get back into that same height away from the planet; in other words you cannot gain anything from gravity.

The problem with the previous scenario is that it considers the planet as a stationary object. However, planets are not stationary. They have a momentum relative to the center of mass of the solar system (let’s assume it to be the center of the sun), therefore you can use a planet to harvest some of its momentum. To do so, you can point your spacecraft behind a planet when it “falls” into the sun for example, and use the planet as a tugboat. During this time, gravity will serve (solely) as the rope connecting the spacecraft and the “falling” planet resulting in some of its energy to pass into the spacecraft by being tugged by the planet. It is not necessary for the planet to be in its “falling” phase (the phase that happens after a planet passes its aphelion), but at any point in the orbit, as long as you can get use of the tug effect.

After the interaction the spacecraft will have a bigger momentum than it should and the planet a little less, causing it to move down into a slightly lower orbit, meaning that the next apogee or aphelion of that planet will be a little closer to the sun.

In conclusion, the extra kick comes from the planet kinetic energy and not from the gravitational force itself.