4

A falling magnet in a copper pipe exerts a Lorentz force on the electrons that participate in the eddy currents a and b. I mean the vertical magnetic force $F = Bqv$, denoted by the blue arrows in the diagram below. The vertical magnetic forces on the eddy currents a and b have the same direction (both downward, independent of the orientation of the magnet).

  • Would this force result in a kind of Hall voltage $V_{AB}$ between the ends of the pipe?
  • Would the formula for the Hall voltage be similar to the usual formula for the Hall effect, $V_\mathrm{H} = \frac{I_x B_z}{n t e}$, from Wikipedia? (Unfortunately, there seems to be no formula to determine $I_a$ and $I_b$, for example as a function of the easily measurable falling speed of the magnet.)

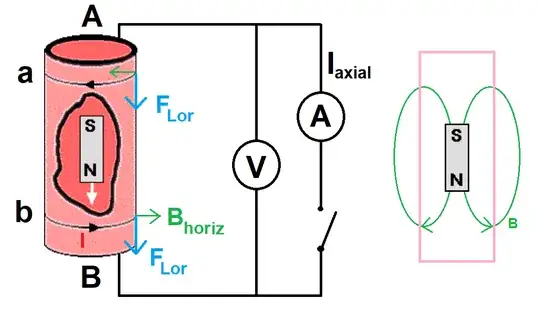
enter image description here

Níck Aguiar Alves
  • 24,192
jkien
  • 2,669

2 Answers2

1

The Hall voltage between the ends of the pipe is

$V = -R_Hmg$

where $R_H$ is the Hall coefficient and $mg$ is the weight of the magnet (in Newtons).

This compact expression arises because, in this configuration, the Hall electric field $E_z = -R_H(J \times B) \cdot \hat z$ has an identical form to the z-directed Lorentz force density $F_z = (J \times B) \cdot \hat z$ and, in the steady state (magnet at terminal velocity), the weight of the magnet, $mg$, is exactly supported by the Lorentz force between the magnet's flux density, $B$, and the eddy current densities, $J$, circulating in the pipe. ($ \hat z$ is the unit vector along the pipe). This result requires circular symmetry and a long, thin pipe.

It's interesting to note that this result is independent of the strength of the magnet and of the diameter and conductivity of the pipe. The terminal velocity will adjust itself until the back-force from the induced eddy currents equals the weight of the magnet. The Hall voltage depends only on the weight of the magnet (and the Hall coefficient).

Roger Wood
  • 2,423
  • 8
  • 21
0

You make a good argument that there should be a Hall voltage across a conducting ring which is shorter than the falling magnet, and that the Hall voltage for the magnet-is-entering eddy current should have the same sign as the Hall voltage for the magnet-is-exiting eddy current. But I don’t think this logic extends to a Hall voltage across the entire conducting pipe, because that sustaining that voltage would require an electric field in regions of the pipe where the eddy current and the corresponding Lorentz force are zero.

I would expect a long magnet falling through a short ring to produce your Hall voltage while the end of the magnet was entering or leaving the ring, but not during the “steady state” period where the body of the magnet is moving through the ring.

For your illustrated setup, where a short magnet falls through a long pipe, I would expect your voltmeter to measure transient Hall voltages as the two ends of the magnet entered and exited the two ends of the pipe. It is not obvious to me whether those four “pulses” of Hall voltage would be the only signal in the detection circuit you’ve shown, and therefore observable using a charge-integrating detector, or whether the field-cancelling motion of charges in the zero-eddy sections of pipe would send “counter-pulses” to your circuit, so that you would have to look for transients.

I used to teach an introductory lab where we measured something like the currents $I_a$ and $I_b$ by having the students shove a bar magnet through a solenoid. (It was not a great lab. Without fail, the students would connect their solenoid to the DC power supply instead of the oscilloscope, with the bar magnet inside, which gave them a fifty-fifty chance of reversing the polarity of their “permanent” magnet.) I can imagine adapting this idea to make a practical implementation of your experiment. A thin copper cylinder, probably with its height comparable to its diameter, with a narrow slit cut in it, and the two sides of the slit connected via low-inductance and low-resistance cable to an ammeter, to measure $I_a$. On the opposite side of the ring from the slit, your Hall voltmeter, connected to the to and bottom of the slit. Your moving magnet should be a good fit to the pipe, and perhaps mounted on some non-magnetic motion stage, so that its velocity can be well-controlled.

rob
  • 96,301