4

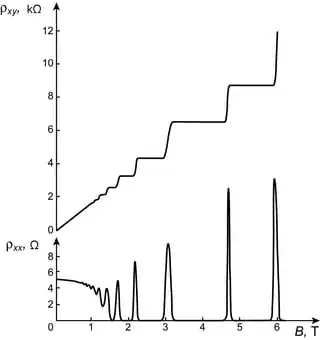
I was wondering why the plateaus of $\rho_{xy}$ in the integer quantum Hall effect are horizontal and do not scale linearly with the magnetic field $B$ since the Lorentz force should still be acting on the electrons.

I understand that by increasing the magnetic field B, new Landau levels become available which contribute to the discrete jumps of $\rho_{xy}$, but those electrons in the Landau levels that are already occupied should be affected by the Lorentz force (which is the underlying mechanism of the classical Hall effect) and hence I would expect them to contribute to a linear scaling of $\rho_{xy}$ as a function of B in between the discrete jumps. Instead of a linear relationship, we can see perfectly horizontal plateaus. Why is that?

enter image description here

xabdax
  • 385
  • 1
  • 10

1 Answers1

1

I guess the question is, given the Hall resistivity as \begin{equation*} R_{xy}=\frac{B}{ne} \end{equation*}

and with $\nu$ Landau levels filled (i.e, density of electrons fixed), why $R_{xy}$ does not go up with $B$.

The simple answer is that the degeneracy of each Landau level also goes up linearly with $B$, so the two contributions cancel:

\begin{align*} R_{xy}=\frac{B}{\nu\times eB/h}=\frac{h}{e^2\nu} \end{align*}

hence a plateau in $R_{xy}$.

Ramal Afrose
  • 143