4

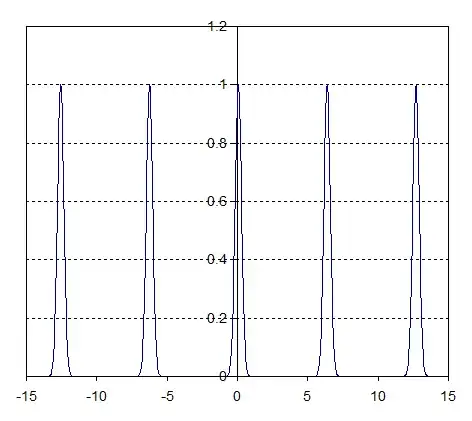
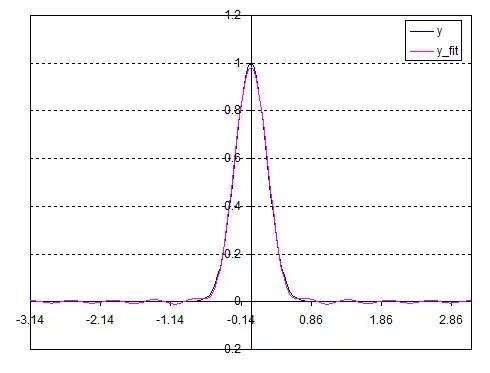
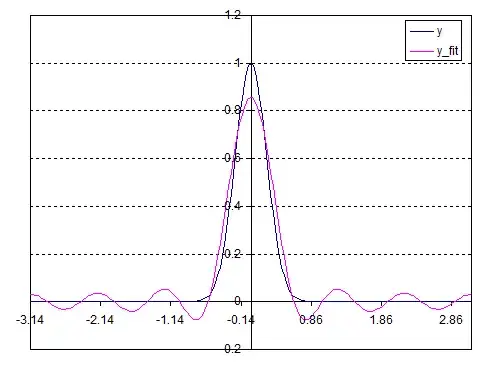
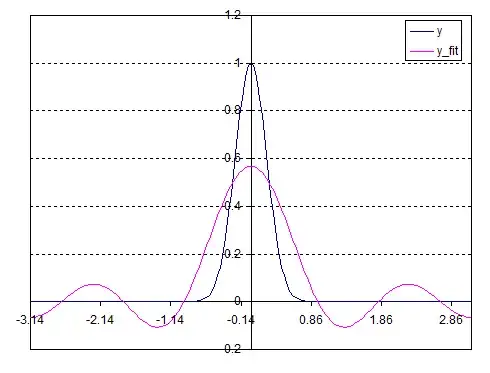
With Fourier-Series Expansion, we can write a function as sum of many non-repating different frequncied different amplituded sine and cosine functions.

Lets assume we know electric-field and magnetic-field representation function of Hydrogen atoms or Iron atoms as a periodic-lattice (If we cannot know, lets take periodic-Dirac-Delta).

Question: how many sine+cosine wave generators do we need to produce such imitation for at least xy plane with minimal erroer(lets say %0.1 about electron-orbit's uncertainity) ? (ofcourse electromagnetic waves are transverse sinusoidal) Very narrow angled generators targeted at same points so they would make a spot of super-positioned waves acting like Iron lattice or whatever em-field needed maybe (even a shield against big objects, with enough power source and strong generators, like in the Star-Trek realm?).

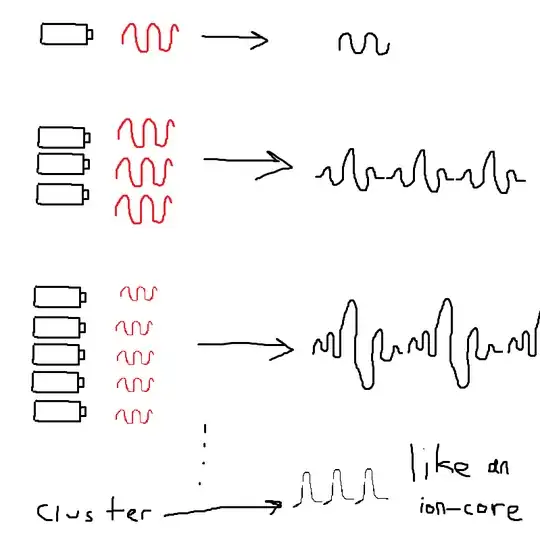
enter image description here

like ion cores in the lattice as a barrier for nano-particles.

Thanks.

huseyin tugrul buyukisik
  • 295

1 Answers1

1

Ok, let's take a gaussian profile, and we'll repeat it every $2\pi$ to turn it into a function for which we can calculate the Fourier coefficients. The resulting function looks like this:

Function

I've written a spreadsheet to calculate the Fourier components for this function and use the components to recalculate the function (I can put the spreadsheet somewhere downloadable if you want).

If I take the first 10 components the fit is close to perfect (with more than 10 components you can't see the difference between the fit and the original function):

10 components

With the first 6 components you can clearly see the difference:

6 components

and with only 3 components the approximation is fairly poor, as you'd expect, though you can already see the central peak developing:

3 components

I'm still not entirely sure what you're asking, but this should give you an idea of how many terms you need to get a reasonable approximation to your target function.

John Rennie
  • 367,598