In this question momentum is conserved along X' direction. But there is a component of mg along the plane which means that there is external force in X' direction. So how is conservation of momentum applied here??
How is conservation of momentum applied even if there is component of $mg$ acting as external force?
3 Answers
Gravity is a non impulsive force. it means it takes enough time to cause action and does not change momentum in an instant. So in time just before and after collision, momentum is conserved and gravity is neglected for such small time.
it will work in all horizontal collisions like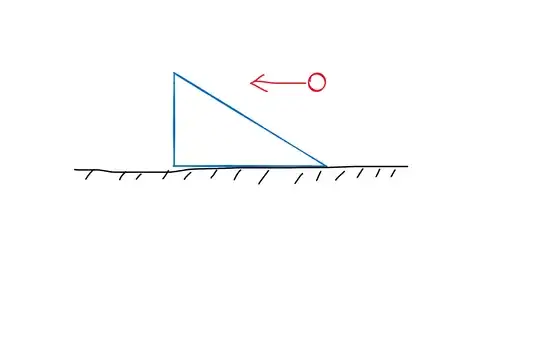
BUT
if ball does not strike horizontally, then Normal and/or friction are impulsive so you cannot conserve momentum even for short durations 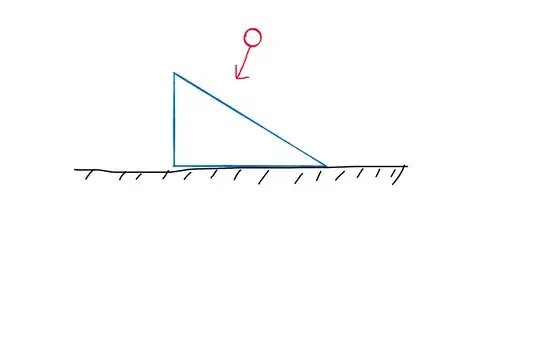
- 409
For the momentum conservation law to be true you must include all interacting parts. You cannot have an external force adding or subtracting momentum out of your system - then obviously momentum isn't conserved for that system. But it is conserved overall, if you included the external part that causes the external force (the planet Earth) in your system.
Compare this with the similarly stated energy conservation law. Energy is always conserved - never destroyed nor brought into existence out of thin air. But obviously, if I define a system that is heated from the outside, then energy is added to my system. Then energy conservation is not fulfilled for my system.
Conservation laws must include all interacting parts to be true.
- 53,191
The momentum is conserved in x direction because there is no external force acting on the center of mass of the ball wedge system, you are correct that the mg component is there along the horizontal but the same force will be applied on the wedge too. Thats why The Momentum is conserved in X direction
- 41
- 3
