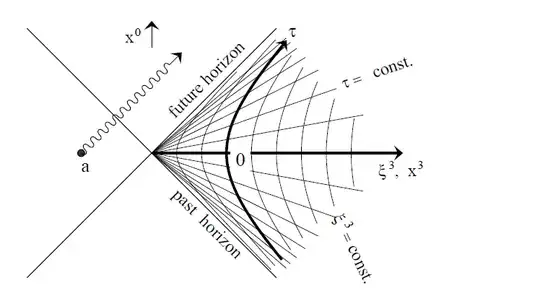
I came across the following statements in 't Hooft's black holes notes, but not being able to justify them.
The metric in the Rindler coordinates $x=\tilde{x}, y=\tilde{y}, z= \rho \cosh{\tau}, t= \rho \sinh{\tau}$ is $$ds^2 = -\rho^2 dt^2 + d\rho^2 + d\tilde{x}^2+d\tilde{y}^2$$
- Gravitational Field Strength
The actual gravitational Field strength felt by the (Rindler)observer is inversely proportional to the distance from the origin.
How can I see this from the metric? How do I mathematically and physically justify this claim?
2. Horizon
Why does the surface $x=t$, act like a Horizon i.e. anything from outside the shaded area shown in the picture can't enter into the shaded region? I think, this can be seen by showing that all time-like curves starting from a point outside the shaded area don't enter the shaded region. But what are all the time-like curves in the Minkowski space-time? and would this assumption still hold for any arbitrary geometry which is locally like the Rindler metric(e.g. the schwarzchild metric near the horizon?)