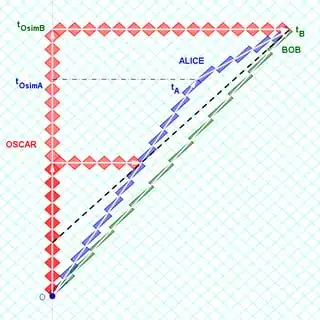
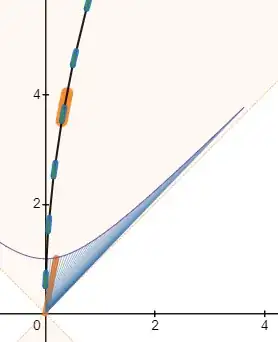
If the laws of physics are the same in all inertial frames why can't we accelerate a particle stationary in its own frame to 0.99c?
Consider a particle that has been accelerated to 0.99c in a particle accelerator in direction d. In the stationary frame of the particle the laws of physics should allow the particle to be accelerated in direction d to 0.99c resulting in a relative speed of 1.98c in direction d from the stationary frame of the particle accelerator.
As others have said, the so called "addition of velocities" (better: "composition of velocities") is not additive, as it is in PHY 101.
Instead
$$V_{CA}=\frac{V_{CB}+V_{BA}}{1+V_{CB}V_{BA}}$$
https://www.wolframalpha.com/input/?i=B%3D0.99%3B+A%3D0.99%3B+%28B%2BA%29%2F%281%2BB*A%29
yields 0.999949 for your velocities.
(This is akin to the fact that slopes of lines don't add. You need a different formula.)
However, what does add are "angles" (which are called "rapidities" in relativity) where $V_{CA}=\tanh\theta_{CA}$
...
so,
$$\theta_{CA}=\theta_{CB}+\theta_{BA}$$
and
$$\tanh(\theta_{CA})\equiv \tanh( \theta_{CB}+\theta_{BA})\equiv
\frac{\tanh\theta_{CB}+\tanh\theta_{BA}}{1+\tanh\theta_{CB}\tanh\theta_{BA}},$$
which is equivalent to the above... but possibly geometrically-simpler to interpret (but may need some practice to accept physically).
https://www.wolframalpha.com/input/?i=B%3D0.99%3B+A%3D0.99%3B+tanh%28arctanh%28B%29%2Barctanh%28A%29%29
yields 0.999949 (the same).
For small velocities, the result is (approximately) additive... since the denominator is approximately equal to 1 in that case.
UPDATE
While this situation (counter to everyday experience) may cast doubt on the correctness Special Relativity, there are many experimental tests of Special Relativity and its implications... and it's done quite well over the range of its applicability.
As starting points,
https://math.ucr.edu/home/baez/physics/Relativity/SR/experiments.html
https://en.wikipedia.org/wiki/Tests_of_special_relativity
UPDATE
Prompted by @PM2Ring 's nested doll sequence comment in another answer,
this visualization of mine might be useful for see what happens
when one does a nested sequence of equal boosts (equal increments in rapidity, in a regular time interval in the instantaneous frame).
One approaches (but never reaches) the speed of light,
and, in the original (lab) frame, it appears that each increment
(naively) appears less effective toward that goal of trying to reach the speed of light.
https://www.desmos.com/calculator/tjngj63cat
People have answered about how the velocities don't add. As to the why they don't add.
Assume that you have frame A, frame B moving at speed v relative to frame A, and object C moving at speed w relative to frame B.
What is the speed of C in frame A? well, in frame B, the object is moving at a speed w as measured with respect to B's time and space. So, in addition to adding the speed w to to the speed v of frame B, there is also a conversion of B's time and space into A's time and space, which is necessary before you can simply add the two velocities together. Thinking about this carefully using the rules of frame transformations ends up at the rules discussed in the other answers.
See https://en.wikipedia.org/wiki/Velocity-addition_formula You're correct up to the point of assuming "resulting in a relative speed of" $.99+.99=1.98$ The original guy still sees the particle moving at $v\lt1.0c$ in his frame of reference, even though the second guy sees it moving at $v=.99c$ in his frame.
You defined the stationary frame to be the frame moving at .99c to the lab frame. If you also define the lab frame to be stationary you have built a logical contradiction into your premise and no conclusion can be valid.
For how to actually work with comparing relative velocities between frames, research "relativistic velocity addition".
