2

I have this dynamical system $$x'=y, y'=-x^3-y+mx$$ and I want to draw the phace space diagram for $m=-1/8, m=1/4,$ the bifurcation points. 1st of all I cant find what kind of bifruction I have( I go from stable focus to stable node and sadle), does it have a name(?). I compute the equilibrium points and theirs stability and i get these phase portraits for $m=-1/8$:

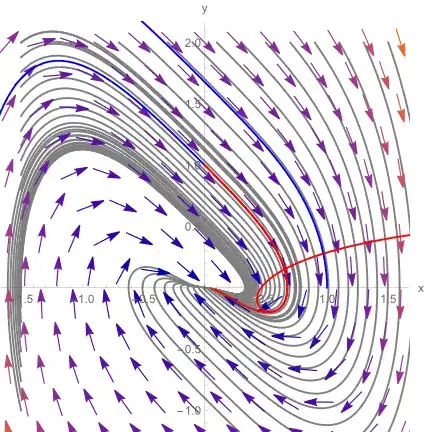
phase portraits for m=1/4

and for $m=1/4$,

phase portraits for m=1/4

which seem wrong. The grey lines are the trajectories, I computed by numerical integration and plotted the corresponding invariant manifolds (blue and red lines).

Lastly I can drop the Mathematica code I used and let you see if I have any mistakes.

https://we.tl/t-8c4XKGoIKY

Qmechanic
  • 220,844
Kostas_vaf
  • 21
  • 1

1 Answers1

1

Could you be plotting the same phase portrait twice instead, the one for $m=1/4$, instead of plotting two different ones for $m=1/4$ and $m=-1/8$?

I used the following little python script I wrote to help me draw phase portraits of planar vector fields:

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

def solve_IVP(vector_field, x_in, y_in, t_stop, resolution):
    s_0 = 0
    s_1 = t_stop
    y0 = np.array([x_in, y_in])
    t_span = np.linspace(s_0, s_1, num=resolution)
    sol = solve_ivp(vector_field, [s_0, s_1], y0, method='Radau', t_eval=t_span)

    return  sol.t, sol.y


def plot_dynamics_and_multi_traj1(vector_field, IVPs, x_left, x_right, x_res, y_down, y_up, y_res, density, normalized):
    '''
    vector_field = the function defining the vector field V to be integrated: 
                   input: x and y (arrays of) coordinates
                   output: a tuple of (arrays of) V_x and V_y calculated coordinates 
    IVP = array of arrays, each row contains: 
       [x_initial, 
        y_initial, 
        t_stop = time to stop, 
        number of discrete points in the time interval from [0, t_stop] (as float)]
    x_res = number of nodes on the x-axis
    y_res = number of nodes on the y-axis
    density = density of blue background trajectories to be drown
    normalized = set to False, unless you want to integrate the unit-normalized 
                 vector field, aligned with the original vector field.

    '''
    if normalized:
      def vf(t, y):
        v = np.array( vector_field(y[0], y[1]) ) 
        return v / np.sqrt(v.dot(v))


else:
  def vf(t, y): 
      return np.array(vector_field(y[0], y[1]))

fig, ax = plt.subplots()
ax.set_aspect('equal') 

x_min = x_left
x_max = x_right
y_min = y_down
y_max = y_up

for IVP in IVPs:
   x_in = IVP[0]
   y_in = IVP[1]
   t_stop = IVP[2]
   res_IVP = int(IVP[3])
   sol = solve_IVP(vf, x_in, y_in, t_stop, res_IVP)
   x_min = min(min(sol[1][0,:]), x_min)
   x_max = max(max(sol[1][0,:]), x_max)
   y_min = min(min(sol[1][1,:]), y_min)
   y_max = max(max(sol[1][1,:]), y_max)
   ax.plot(sol[1][0,:], sol[1][1,:], 'r')
   ax.set_aspect('equal')  

x, y = np.meshgrid(np.linspace(x_min, x_max, x_res), 
                   np.linspace(y_min, y_max, y_res))

Vx, Vy = vector_field(x, y)

if type(Vx) != object:
    Vx = Vx * np.ones(x.shape, dtype=float)
if type(Vy) != object:
    Vy = Vy * np.ones(x.shape, dtype=float) 

ax.streamplot(x, y, Vx, Vy, density=density)

plt.grid()
plt.show()

return None

and applied it to your vector field

$$\vec{\text{VF}}(x, y) \, =\, y \, \frac{\partial}{\partial x} \, +\,\big( -x^3- y + m\, y \, \big)\frac{\partial}{\partial y}$$

# equations defining the vector field:
def VF(x, y):
  return (y,  -x**3 - y - m*x)

I set up a list of starting points selected horizontally over and under the x-horizontal axis (initial value parameters IVPs):

# bifurcation parameter
m = 1/2

how many equally spaced nodes to select along the x-axis


x_res = 100


how many equally spaced nodes to select along the y-axis


y_res = x_res


the right endpoint of the plot on the x-axis


x_size=0.5


the top endpoint of the plot on the y-axis


y_size=0.3


for how much time to integrate the trajectories


stop_time = 12


number of points along each trajectory to be used for integrating the equations


sample_points_on_trajectory = 500


setting up the initial values:


choose an array of initial points for a finite number of solution trajectories:


set up the x-coordinates of the initial points:


IVPs =np.arange(-x_size, x_size, 2*x_size/10)
IVPs = np.concatenate((IVPs, - IVPs), axis=0)


set up the initial value parameters:


row1 = x-coordinates of initial points


row2 = y-coordinates of initial points (left empty for now)


row3 =


IVPs = np.array([IVPs, 
                 np.empty(len(IVPs), dtype=float), 
                 stop_time * np.ones(len(IVPs), dtype=float),
                 sample_points_on_trajectory * np.ones(len(IVPs), dtype=float)])


initializing row2 = y-coordinates of initial points:


below the x-axis


IVPs[1 , 0:int(IVPs.shape[1]/2)] = - y_size


above the x-axis


IVPs[1, int(IVPs.shape[1]/2): IVPs.shape[1]] = y_size


transpose the initial value parameters:


IVPs = IVPs.T

and plotted the following two phase portraits: $$m = \frac{1}{4}$$

# bifurcation parameter
m = 1/4

plot the phase portrait:


plot_dynamics_and_multi_traj1(VF, IVPs,-x_size, x_size, x_res,
                                       -y_size, y_size, y_res, 
                                        density=0.7, normalized=False)

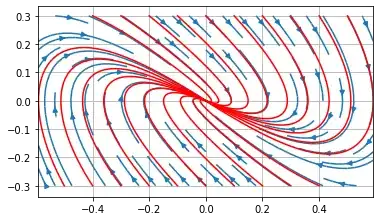
enter image description here

and $$m = -\,\frac{1}{8}$$

# bifurcation parameter
m=-1/8.

plot the phase portrait:


plot_dynamics_and_multi_traj1(VF, IVPs,-x_size, x_size, x_res,
                                       -y_size, y_size, y_res, 
                                        density=0.5, normalized=False)

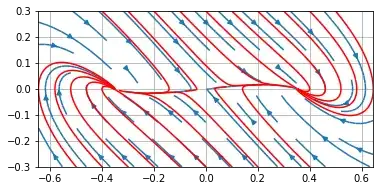
enter image description here

As you can see, when the bifurcation parameter $m$ goes from positive to negative values, the stable equilibrium point changes from being asymptotically stable focus to three equilibria, one saddle point in the middle and two symmetric stable nodes.

Futurologist
  • 2,621