2

I am trying to simulate a ball bouncing on an inclined surface. And I am thinking about how friction play during the collision.

When there is no friction, at collision, we can exclude the force to find the velocity afterwards by using the momentum. velocity along the normal direction of surface is $e* v * \cos(\alpha)$, where $e$ is the restitution coefficient and the $\alpha$ is the angle between the incident vector and normal.

and the velocity along the surface is $v * \sin(\alpha)$.

The collision is an instant stage, where the contact happens in a very short time ($\delta t$). I assume the friction would cause some loss of energy but by how much? The friction force can be calculated by using the impulse formula. But I need to know if the friction would affect the momentum(in this case, the velocity) The reason I want to do it is that the friction could make the ball spin during bouncing.

Thanks for the help.

Roger V.
  • 68,984
BruceZ
  • 31

3 Answers3

1

The free-body diagram at exact collision time should look like:

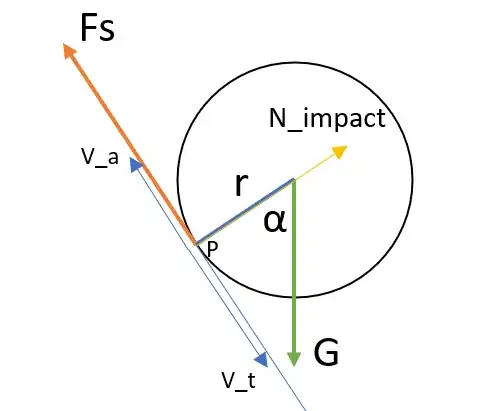
![enter image description here

If I assume there is no mass loss the first equation cannot be used, otherwise, J would always be zero.

I will define some parameters:

e: coefficient of restitution

u: coefficient of friction

t_c : time collapse during collision

vi: initial velocity before collision

vf: final velocity after collision

Fs is the friction force and N_impact is the impact force

$N_{impact} = m*(vf-vi)/t_c$

$|Fs| = |u*N_impact|$(this donates only magnitude is calculated)

the direction of Fs is calculated by the instant velocity of the contact point P. The system translation velocity is separate from the self-spinning angular velocity. So the contact point would be simultaneously experiencing system velocity v_t, going downwards along the surface, and the backward velocity $v_a$ caused by angular velocity. The friction force is at the opposite direction of $v_a + v_t$.

I don't really understand the calculation of angular velocity $\Delta \omega$. Sadly, I don't have enough reputation to ask in the original post.

\begin{aligned} \Delta\vec{\omega}_{1}&=-I_{1}^{-1}\left(-\vec{c}_{1}\times\hat{n}\right)J&\Delta\vec{\omega}_{2}&=+I_{2}^{-1}\left(-\vec{c}_{2}\times\hat{n}\right)J \end{aligned}

Why is he using the cross product between centre of mass and the contact normal? what does the

BruceZ
  • 31
0

Friction is a rather general word, which can mean several things here.

  • The dissipation processes that reduce the energy of the ball when it heats the surface, by transforming a part of this energy into heat.
  • Friction of the ball against the air, which slows it down.
  • Sliding friction when it touches the surface: it may actually force the ball to start rolling instead of bouncing back - and interesting physics problem to think about.
  • Finally, rolling resistance is probably also involved, as the ball does not necessarily stay at the same place while it is in the contact with the surface.
Roger V.
  • 68,984
0

So during a typical collision calculation with no friction, there is a single impulse $J$ along the contact normal that is applied in equal and opposite measure on the colliding bodies. This impulse is calculated by

$$ J = (1+\epsilon)\, m^\star\, v_{\rm imp} $$

where $\epsilon$ is the coefficient of restitution, $m^\star$ is the reduced mass of the system and $v_{\rm imp}$ is the impact speed.

For your situation where friction (and rotation) are important you have two impulses acting, $J_n$ for normal impulse (as above) and $J_t$ for frictional impulse.

fig1

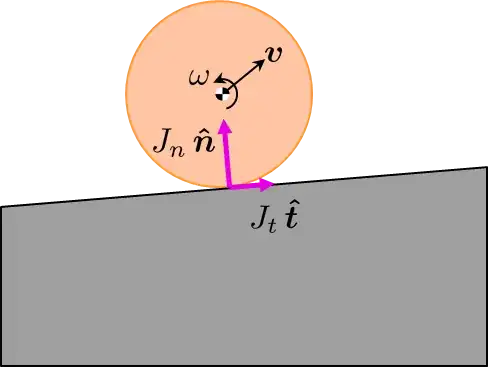
The reduced mass calculation is different for both impulses because they act on different directions. Use the link above to get the equation for calculating each of the reduced massed based on the directions $\boldsymbol{\hat{n}}$ and $\boldsymbol{\hat{t}}$.

$$m_{\rm reduced} = \left[\tfrac{1}{m_{1}}+\tfrac{1}{m_{2}}+\left(\hat{n}\times\vec{c}_{1}\right)\cdot I_{1}^{-1}\left(\hat{n}\times\vec{c}_{1}\right)+\left(\hat{n}\times\vec{c}_{2}\right)\cdot I_{2}^{-1}\left(\hat{n}\times\vec{c}_{2}\right)\right]^{-1}$$

Here you can assume the object is hitting the ground and so $\tfrac{1}{m_2} = 0$ and $I_2^{-1} = 0$ to simplify the above a bit. Further simplifications exists for 2D problems (also in the link above).

Also the impact speed is different for the directions, and again the link above has the equation needed to calculate those.

$$v_{{\rm imp}}=\hat{n}\cdot\left(\vec{v}_{1}+\vec{c}_{1}\times\vec{\omega}_{1}-\vec{v}_{2}-\vec{c}_{2}\times\vec{\omega}_{2}\right)$$

The third part is a bit debatable. What coefficient of restitution to use for frictional impulse? Is it the same as the value to be used for bounce? Is it 0, or is it 1. I remember a discussion in this forum about this and it was stated to use $\epsilon_t = 1$ which is counter intuitive at first but might match data takes from supper bouncy balls.

I recommend you play around with this and find something that produces reasonable results.

Once the impulses are calculated, then again the link above has the equations of how an impulse will change the motion of the body. I am modifying the above to include both impulses

$$\begin{aligned} \Delta\vec{v}_{1} & =-\tfrac{J_n \hat{n} + J_t \hat{t}}{m_{1}}&\Delta\vec{v}_{2} & =+\tfrac{J_n \hat{n} + J_t \hat{t}}{m_{2}}\\ \Delta\vec{\omega}_{1} & =-I_{1}^{-1}\left(-\vec{c}_{1}\times(J_n \hat{n} + J_t \hat{t})\right)&\Delta\vec{\omega}_{2} & =+I_{2}^{-1}\left(-\vec{c}_{2}\times(J_n \hat{n} + J_t \hat{t})\right) \end{aligned}$$

References

jalex
  • 3,765