What is the direction of angular momentum? Are Torque and angular momentum same?

Question

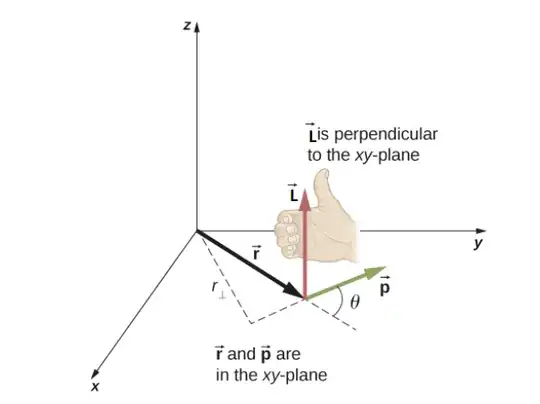
I just started learning in my class 11 physics book, where I find Torque and angular momentum. After reading the definition, I am confused about are Torque and angular momentum are same? If not what is the difference between them? Lastly what is the direction of angular momentum?

Answer 1

No, torque and angular momentum are different physical quantities. They don't even share the same units.

The instantaneous angular momentum $\vec {\bf{L}}$ of a particle relative to an axis through the origin is defined by the cross product of the particles instantaneous position vector $\vec{\bf{r}}$ and its instantaneous linear momentum $\vec{\bf{p}}$: $$\vec {\bf{L}} = \vec{\bf{r}} \times \vec{\bf{p}}$$ The net external torque about the same fixed axis in an inertial frame is then $$\sum \vec{\bf{\tau}} = \frac{d\vec {\bf{L}}}{dt}$$

The direction of the angular momentum vector is the direction of $\vec{\bf{r}} \times \vec{\bf{p}}$, which can be found from the right hand rule.

Hope this helps.

---

Image source

Answer 2

As we are aware about the force. It's same with the torque, unofficially we can call it as a Rotational Force for better understanding. Which is equal to

$τ = I × α $

Where I is moment of inertia and α is angular acceleration.

let's take an example if you will try to rotate the spring vertically about it's axis let's say clockwise about it's axis you will feel that something is trying to rotate your hand anticlockwise that's the torque, Which is trying to rotate your hand anticlockwisely.

And angular momentum is noting but just a product of it's moment of inertia and the angular velocity.

Let's take an example to understand what's this thing, so when you turn off the rotating fan why does it still rotates even if the motor is turned off. That's because of the angular momentum. It stops slowly because of the heat losses due to friction ,air resistance etc.

So we can say that the angular momentum is something the keeps the object in the circular motion.

Post edit:- the direction of the angular momentum will be same as the direction of angular velocity.

Answer 3

I am going to try to answer plainly and avoid using vector algebra and concepts like the cross product.

I assume you are familiar with the concept of torque as a force at a distance. If not, read about torque as the moment of force with the example of balancing a see-saw. The main takeaway here is that the perpendicular distance to the line of action of the force is what is important for torque.

Angular momentum is similarly defined as momentum at distance (moment of momentum, vs. moment of force). Angular momentum tells us that something carrying momentum is at some distance away. Similarly, the perpendicular distance to the line of action of momentum (called the percussion axis) is what is important for angular momentum.

Just as you can combine two offset forces that cancel each other out, except still produce a pure torque (what is called a force couple), you can combine two moving masses that their momentum cancels out, to produce pure angular momentum.

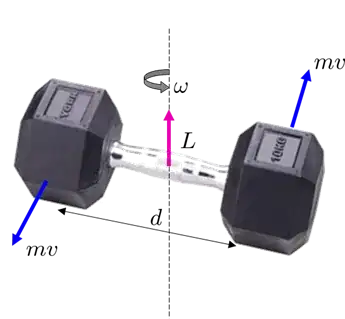
$$ L =\left( \tfrac{d}{2} m v \right) + \left( \tfrac{d}{2} m v \right) + d\,(m+m)\,\omega \tfrac{d}{2} = m d^2 \omega $$

Just as the concept of conservation of linear momentum is important, the concept of conservation of angular momentum is important also. Since angular momentum is momentum at a distance, if angular momentum is conserved it means the perpendicular distance is conserved as well as the magnitude of momentum.