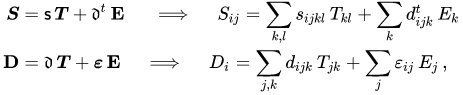The equations that you are presenting in your questions are not "the equations" for piezoelectricity. These are termed constitutive relations. You are missing the "definition" of the electric field in terms of the potential, the definition of the strain in terms of displacement, and the conservation equations.
Following, I will rewrite the equations.
The constitutive equations are (the inverse of yours):
\begin{align}
T_{ij} = c_{ijkl} S_{kl} - e_{kij} E_k\, \\
D_i = e_{ijk} S_{kl} + \epsilon_{ij} E_j\, .
\end{align}
The electric field and strain are written as:
$$E_k = -\phi_{,k}\, ,\quad S_{kl} = \frac{1}{2}(u_{k,l} + u_{l, k})\, ,$$
being $\phi$ the electric potential and $u$ the displacement.
You can write the (conservation) equations using the above information to obtain
\begin{align}
c_{ijkl} u_{k, lk} + e_{kij} \phi_{,kj} + f_i = \rho \ddot{u}_i\, ,\\
e_{ikl} u_{k, li} - \epsilon_{ij} \phi_{,ij} = \rho_e\, ,
\end{align}
where $f_i$ is the body force, $\rho$ is the mass density, and $\rho_e$ is the charge density.
You could say that the last equations are the equations "of motion" for the material.