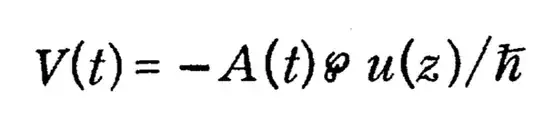I'm reading electrodynamics physics notes that describe the polarization of a medium. The notes describe the active atoms as having two levels $a$ and $b$, separated by energy $\hbar \omega$ and represented by a density matrix $\rho$. The atoms are stationary.
The equation of motion of the density matrix is
$$\dot{\rho} = -i[H, \rho] - \dfrac{1}{2}\left(\Gamma \rho + \rho \Gamma \right) + \lambda,$$
where
$$\rho = \begin{bmatrix} \rho_{aa} & \rho_{ab} \\ \rho_{ba} & \rho_{bb} \end{bmatrix}, \ \ \ \ \ H = \begin{bmatrix} W_{a} & V \\ V & W_{b} \end{bmatrix}, \\ \Gamma = \begin{bmatrix} \gamma_{a} & 0 \\ 0 & \gamma_{b} \end{bmatrix}, \ \ \ \ \ \lambda = \begin{bmatrix} \lambda_{a} & 0 \\ 0 & \lambda_{b} \end{bmatrix}$$
The notes then state that the perturbation Hamiltonian is $\hbar V$, and the unperturbed energies of the levels are $\hbar W_a$ and $\hbar W_b$. Furthermore, the two levels decay with damping constants $\gamma_a$ and $\gamma_b$, and are populated by pumping at rates $\lambda_a$ and $\lambda_b$.
Therefore, using the Fourier expansion of the electric field $E(z, t) = \sum\limits_n A_n(t) u_n(z)$, where $u_n(z) = \sin(k_n z)$ and $k_n = \dfrac{n \pi}{L}$, the notes claim that the electric dipole approximation for the perturbation becomes
I've included the image of the equation because I don't actually understand what that symbol between $A(t)$ and $u(z)$ is (I can't find it as a LaTeX symbol, and I've never seen it before). What is this symbol and how was it part of this derivation?
Relevant: Quantum Mechanical Electric Dipole Hamiltonian
$$V(t) = - \left( \sum_j \dfrac{q_j}{m_j} \left( \hat{\epsilon} \cdot \hat{p}_j \right) \right) \dfrac{E_0}{\omega} \sin(\omega t) \tag{7.3.13}$$