-2

A lot of the explanations of the Twin Paradox rely on acceleration, non-inertial frames, and/or curved/kinked world lines to break symmetry and therefore explain why the traveling twin ages less than the stationary twin.

But doesn't the traveling twin, T, age less even if he only flies away in a perfectly straight line with no acceleration, no changes to his inertial frame, and no curved/kinked world line at all?

If that's true, then why can't we put ourselves into T's inertial frame instead and come to the opposite conclusion? T is now stationary and the previously stationary twin, S, is now moving inertially. Can't we reason similarly and assert that S should now age less than T? That seeming contradiction seems to be the crux of the twin paradox for me at least.

So what happens when we cut the Twin Paradox problem in half? Let's eliminate all acceleration, non-inertial frames, and curved/kinked world lines so that they can't possibly be explanations for time passing at different rates for twin clocks.

I want to first demonstrate in S's frame that T really does age less even just with relative inertial motion. So, let's first adopt the inertial frame of clock S.

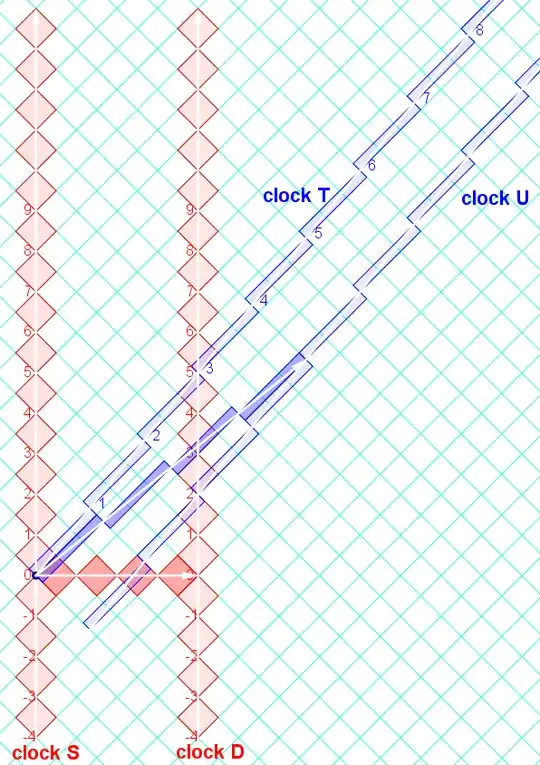
Clock D is 4 LY distant from S and has zero velocity relative to S. Let's synchronize S and D such that when S = 0, then S also observes distant D = -4 years.

Now suppose another clock T is moving with constant velocity of 0.8c in S's frame towards D. At S = 0, T coincides with S and also happens to have T = 0.

S calculates that T will coincide with D when S = 5 years.

Einstein and Lorentz teach that in T's frame T = 3 years when T coincides with D.

Because clocks S and D are synchronized, in D's frame D = 5 years when T coincides with D.

At T = 0, T sees S = 0 at 0 distance. At T = 3 years, T sees D = 5 years at 0 distance. T knows (was told) that S and D have synchronized time in their frames. Doesn't this mean that T knows S and D have experienced the passage of more time (5 years) than T did during its journey from S to D (3 years)?

Based on this information, can't STD all agree that time actually ran only 60% as fast for T as it did for both S and D during T's journey from S to D?

Here's my question: assuming we can correctly say all of that, then why can't we reformulate the scenario entirely from T's inertial frame and similarly reason that because S and D are moving relative to T, that STD will all agree that S's and D's clocks ran slower than T's?

We can also analyze this situation from what each clock observes during the journey if that helps. Let's say that all the clocks are continuously radio broadcasting their values from long before S and T coincide to long after T and D coincide.

Let's first describe what S observes about D and T.

At S = 0, S observes D = -4 years and T fly through with T = 0 at distance 0. As T flies away from S, S observes that T's clock is running 3 times slower than itself.

At S = 9 years, S observes D = 5 years and T = 3 years at a distance of 4 LY.

At S = x years (s.t. x >= 0), S observes D = x - 4 years and T = x/3 years at a distance of x * 4 / 9 LY.

Now, let's describe what D observes about S and T.

At D = 4 years, D observes S = 0 and T = 0 at a distance of 4 LY. As T flies towards D, D observes that T's clock is running 3 times faster than itself.

At D = 5 years, D observes S = 1 years and T = 3 years at a distance of 0.

At D = x years (s.t. x <= 5 years), D observes S = x - 4 years and T = 3x - 12 years at a distance of 20 - 4x LY.

At D = 0 years, D observes S = -4 years and T = -12 years at a distance of 20 LY.

Interestingly, T appears to D to be traveling at 4 times the speed of light (i.e. - traveling 4 LY in 1 year of D's time). Of course, that's not what is actually happening. As T approaches the speed of light, then T will appear to D to cover more and more distance per unit of D's time. At the limit, T will appear to be moving with infinite speed towards D. This is just a consequence of T chasing the speed of light towards D and, therefore, compressing the information about its position into less and less of D's passage of time. If a distant cataclysmic event is moving towards us at the speed of light, then it will run through us before we can even detect its existence.

Finally, let's describe what T observes about S and D. I might get this part wrong.

At T = 0, T observes S = 0 at distance 0 and D = -4 years at distance 2.4 LY.

At T = 3 years, T observes S = 1 years at distance 2.4 LY and D = 5 years at distance 0.

In T's frame, T observes S's clock to run 3 times slower and observes D's clock to run 3 times faster than T's clock.

All of this demonstrates the seeming "paradox" that both S and T observe each others' clocks running 3 times slower than their own as they move away from each other, but when they make a direct comparison of their clocks at distance 0 (via D's synchronized clock) they all agree that less time has passed for T than S.

Is that the (half) twin paradox explained without invoking any kind of acceleration, non-inertial frames, and/or curved/kinked world lines???

I still don't fully see how this answers my original question though. Can't we reformulate the scenario entirely from T's frame and reason similarly that the now moving clocks S and D should actually run slower (i.e. - via direct comparison of T and D at distance 0)?

The scenarios seem to be the same in the sense that T and D are moving towards one another in both frames, so they will each see the other's clock running 3 times faster than their own clock. Similarly, both S and T are moving away from one another in both frames, so they will each see the other's clock running 3 times slower than their own clock.

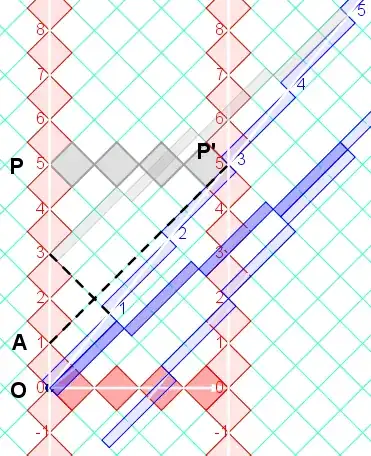
Here's a shot in the dark: Is the asymmetry entirely due to the Lorentz length contraction in T's frame while the passage of time in SD's frame is not affected?

EDIT: Thank you all for the kind feedback! Here are a few things I learned through your answers and comments:

  1. Yes, you can flip my example around and come to the opposite conclusion. STD all agree that less time passed for T in S's frame. STD also all agree that more time passed for T in T's frame. That's symmetric relativistic time dilation.
  2. The answer to the Twin Paradox really is curved/kinked world lines for the traveling twin breaking relativistic symmetry. This can also be described as acceleration, non-inertial frames, and/or frame switching for the traveling twin.
  3. You can cut the Twin Paradox in half, somewhat like I supposed, simply by making T match D's velocity when they coincide. That will put T in S's (and D's) inertial frame and the traveler really will have only aged 3 years while S and D have aged 5 years. T's world line will then have a kink in it in all frames. People might argue that example is less tricky and complex than the original Twin Paradox. That's probably true, but the answer to both versions is the same.
  4. I was implicitly preferring S's frame and using it as my "yardstick." T's frame is every bit as valid and deserved a deeper evaluation of events from T's perspective. The main thing I was goofing up is how the passage of time / simultaneity works in T's frame.
jschultz410
  • 122

5 Answers5

6

The time dilation effect is entirely symmetrical. When a given time, say 3 years, has passed for the travelling twin, the local time in the Earth's frame of reference (ie local to the travelling twin) will be greater than 3 years. Likewise when 3 years have passed for the stay-at-home twin, the local time (ie at Earth) in the travelling twin's frame will be greater than 3 years. You need to take the relativity of simultaneity into account.

In your own attempted explanation, you are making the task more complicated by imagining what S and D see from a distance. There is no need for that, and you have confused yourself by taking it into account.

Time dilation arises because the planes of simultaneity of S and T are tilted relative to each other. If you imagine that T is towing a long line of clocks, each of which is synchronised in T's frame, those clocks will all appear our of synch in S's frame, just as all the clocks in S's frame seem out of synch to T.

If we take the specific scenario you outlined, when T arrives at D with 3 years showing on T's clock and 5 years showing on D's clock, the moment of T's arrival is simultaneous in the Earth's frame with a time of 5 years showing on S's clock, just as it does at D. However, those two events are not simultaneous in T's frame. When 5 years shows on the clock at S, a passing clock trailed by T will show 8.33 years. Likewise when 3 years first showed on the clock at S, a passing clock trailed by T would show 5 years, so the clock at S seems time dilated in T's frame just as the clock at T seems time dilated in S's frame. In fact, all the clocks tick at exactly the same rate- the effect of time dilation arises from the fact that the time axes of the two reference frames are tilted relative to each other.

Professor Sushing
  • 29,350
3

You are mixing a few things up. To synchronise two clocks S and D, S has to send a signal to D first (because D and S are not in the same location), and make it active such that S and D become synchronized.

Here is the catch: It doesn't matter when or how S does this, in S' frame (who has been moving with velocity vx with respect to S since the eternity) D and S remain unsynchronized. For example, assume that at S(t=0), S and S' are in the same location and their clock is synchronized. Also S has put a laser between him/herself and D at L = 2Ly. Now, if at S(t=-2y) this laser becomes activated and send a signal toward S and D at the same time (since laser is at rest with respect to S and D) according to S, D and S clocks two years later become active at the same time, so they will be synchronized. According to S' however, the light signal arrive at D much much sooner than S because after all D is moving toward the light signal while S is moving further away from it (you can use Lorentz transformation for time as well, it gives the sane result), thus S' claims that D and S are not synchronized and D has been activated a lot sooner than S. So even though S' might see D shows 5y, but he doesn't conclude that S shows 5 year too, because after all S has been activated a lot later than D so S' says that nope, S is still younger than me. And that's because of perfect symmetry betwern S and S'. So your problem is assuming that S' consider S and D synchronized, while it's not true.

Paradoxy
  • 1,427
2

Your mistake is that you do not understand all the complexity of the Lorentz transformation. It does mix time and space in a much more complicated way than you think.

First I want to correct some mistakes of some other answers. Since S and D are in the same inertial frame their clocks can indeed be synchronized, they can first leisurely measure their relative distance, 4 LY. Then S sets its clock at t=0 at the precise time T passes in front of S with V=0.8c. S immediately sends a signal, telling D it is 0 for him; on reception D sets his clock at 4 years, and immediately confirms to S and S gets D's signal at time 8 years, no problem at all.

Assume T is in a huge spaceship, more than 12 LY long, say.

Because of length contraction, at the instant T passes S, the point of T's spaceship facing D when D's clock says t=0 is not the point 4 LY ahead of T in T's frame for instance as written on T's spaceship. This point, at the time when in the frame of S and D, all synchronized clocks of that frame show zero, is only 2.4 LY from S. The point in front of D at that time must be at 6.666 LY as written on T's spaceship so that length contraction makes it appear to be at 4 LY from S, just in front of D. But of course all the distances written on T's spaceship appear wrong to all observers in S and D frame.

Now is the very important point.

For all observers in the frame of S and D, T is at 4 LY from D, propagating at 0.8c and reaches D after 5 years. And because of time contraction, D knows that, if T's notes down the time ${\frak {t}}$ at its clock "in passing" with S when they cross, then it will only register 3 years more by the time it reaches D.

But what time is it now in T's spaceship at the point U just fronting D ?

It cannot be ${\frak {t}}$ !

On T's spaceship, this point U it is 6,6666 LY from T. The frame of S and D is moving at speed -0.8c, so it is contracted. For all the observers in T's spaceship, the lengths, as written on the frame of the frame of S and D ,are wrong. The length on the frame of S and D till the point facing point T, 6,6666 LY away, must read as 11,1111 LY not just 4 LY away as S is ! In T's spaceship, at the time ${\frak {t'}}$ when D is seen showing time t=0 in front of U, T is still very, very far from S. Or, rather, S is still very, very far from T because T is fixed and S is moving towards T. So this instant, when D at t=0 crosses U, is at a time ${\frak {t'}}$ long before ${\frak {t}}$

How long will it take, as seen from T's spaceship, for D to reach T ? D is facing U, 6,6666 LY away from T. At speed 0.8c, it will take 8.3333 years. Of course, because of time contraction for D it will only take 5 years. As expected !

But the point is that even though clocks on the frame common to S and T clocks can perfectly be synchronized, there is something that does not happen as you expect. The events "T passes S" and "U passes D" are at the same time $t=0$ in that frame but not at the same time in the frame of T and U.

In that frame, if T passes S at ${\frak {t}}$, T passes D at ${\frak {t}+3}$ But if D passes U at ${\frak {t'}}$, then D passes T at ${\frak {t'}+8.33333}$ which is the same as ${\frak {t}+3}$ since it is the same event.

Therefore ${\frak {t'}=\frak {t}-5.33333}$

T is still very very far from S when U passes D, or, rather, S is still very very far from T when U passes D as seen in the spaceship of T and U.

Two events that are not at the same place can be seen as simultaneous in one frame (that of S and D) but different in another one (that of T and U).

Alfred
  • 4,546
2

Summary of below:

  • Your numerical calculations seem correct. They are in accord with a spacetime diagram I drew.
  • After clarifying some terms, I re-interpret some of your calculations.
  • There is no clock effect or twin paradox to consider since there is no reunion event.

"A spacetime diagram is worth a thousand words."

This spacetime diagram is useful in verifying and clarifying all of your measurements. A diamond represents the light-signals in one tick of a light-clock carried by an inertial observer, and it provides the tickmarks in time and space for that observer. By Lorentz-invariance (since the determinant of the boost is 1), the areas of these "clock"-diamonds are equal. The "rotated graph paper" helps us draw the diamonds and do calculations.

Note that the timelike-diagonal of a diamond is along the worldline,
and the spacelike-diagonal is parallel to the line (hyperplane) of simultaneity for that worldline. That the spacelike-diagonals of all diamonds are not all parallel is the relativity of simultaneity.

I have introduced "clock U" to be analogous to "clock D".

robphy-RRGP-CuttingTheTwinParadox

For instance,

Clock D is 4 LY distant from S and has zero velocity relative to S. Let's synchronize S and D such that when S = 0, then S also observes distant D = -4 years.

Your "when S = 0, then S also observes distant D = -4 years"
means "When the clock-S reads 0, it receives a light-signal from clock-D emitted when clock-D read -4." So, S "sees" the images of S's 0-tick and D's (-4)-tick.
In your post, "observes" means "receives a light-signal".

On the diagram, draw the past light-cone [along the grid lines] of event O (where inertial clocks S and T met). The past-cone meets clock-D when clock-D read -4.

All of your numerical values are consistent with this diagram.
So, that's good.

Some comments on terms. [In (1+1)-Minkowski spacetime...]

  • proper-time of a worldline segment: the elapsed time on wristwatch carried along that worldline. This time is used to assign the "length of the worldline-segment in Minkowski spacetime"... [and in a Galilean spacetime].

  • time-dilation relates two spacelike-related events on inertial worldlines that met at one event (call it O). The measurer is usually interested in a distant event P' and uses a local event P on her worldline that she says is simultaneous with distant event P'. (See the diagram below.)
    OP is the timelike leg of a Minkowski-right triangle, and PP' is the spacelike leg orthogonal to OP. OP' is the timelike hypotenuse. If $\theta$ is the rapidity-angle between OP and OP', then OP is the adjacent side. The time dilation factor is the "ratio of the apparent time-difference between O and P' " Clock-S said that $OP'$ took [has a time-component] 5 years, while Clock-T who experienced both O and P' said $OP'$ took [has a time-component] 3 years.

$$\gamma=\cosh\theta=\frac{adj}{hyp}=\frac{OP}{OP'}=\frac{5}{3}, \mbox{ where } v=\tanh\theta=\frac{opp}{adj}=\frac{PP'}{OP}=\frac{4}{5}.$$

As others have noted, this is a symmetric situation between two inertial observers.
Although P and P' are not simultaneous according to the other observer (like clock-T), there is another pair of events that are simultaneous to that observer. That observer will determine the same time dilation factor.
One can draw the analogous diagram above in the frame where clock-T is at rest. But one can learn to read the relations off of the diagram in the S's frame. (See the diagram below with additional features. Can you see the 5-4-3 triangle that is Minkowski-isometric to OPP' with legs parallel to T's diamond-diagonals and hypotenuse 3 on S's worldline?)
This answers your first question.

  • Clock effect: Between two [timelike-related] events (say O and Z), the elapsed wristwatch time of a worldline from O to Z depends on particular worldline. The inertial worldline from 0 to Z logs the most elapsed time, while any other worldline from 0 to Z logs a shorter elapsed time.

    In the simplest case, this is akin to the triangle-inequality in Euclidean geometry, but it's reversed in Minkowski spacetime: the inertial-worldline OZ is longer than the sum of the "lengths" (as measured by their wristwatches) of the other two legs, OQ and QZ (two inertial-legs which form a non-inertial worldline OQZ).

    It can be interpreted here as two sequential time-dilation problems,
    and is likely the reason for the title of the OP's question.
    Note: if there is no separation event and reunion event between the two clock-worldlines,
    there is no clock effect (and no twin paradox) to discuss.

  • Twin Paradox: Assuming the Clock Effect is established, the so-called paradox is the attempt to study the problem from view of the non-inertial observer, somehow claiming equivalence with the inertial observer by invoking the principle of relativity. If successful, then this would invalidate the clock effect--leading to no route-dependence of elapsed proper time from O to Z.

    This effectively takes the triangle above and straightens the bent path, but at the expense of breaking the inertial leg and making it discontinuous. (Details at https://physics.stackexchange.com/a/507592 .)

    The Euclidean analogue of this like trying to make the two legs of the original triangle straight and forming a triangle that would analogously satisfy a similar triangle inequality.... but this too would come at the expense of breaking the initially straight segment and making it discontinuous.

    My punchline for the Twin Paradox: "Being able-to-be-at-rest" ≠ "Being inertial".

Again, in your question, there is no clock effect (and no twin paradox) to discuss.*

  • Doppler effect relates two lightlike-related events on inertial worldlines that met at one event (call it O) (or, more generally, a pair of events on one worldline that are (both future- or both past-) lightlike-related to a pair on the other worldline). This is the ratio of the period of signal-reception to the period of signal-transmission.

    This is featured when you say

At S = 0, S observes D = -4 years and T fly through with T = 0 at distance 0. As T flies away from S, S observes that T's clock is running 3 times slower than itself.

On the diagram below, the Doppler factor $$k=\exp\theta=\frac{OP'}{OA}=\frac{\Delta t_{rec\ by\ T}}{\Delta t_{trans\ by\ S}}=\frac{3}{1}=3.$$ $$k=\exp\theta=\frac{\Delta t_{rec\ by\ S}}{\Delta t_{trans\ by\ T}}=\frac{3}{1}=3.$$ I would not describe it as you do "T's clock is running 3 times slower".
I would describe it as above: the ratio of reception-period to transmission-period.

(By the way, this "3" is the reason T's diamonds are stretched in one direction by a factor of 3 and shrunk in the other direction by a factor of 3 (to keep the area unchanged). $k$ and its reciprocal are the eigenvalues of the Lorentz boost transformation.)

robphy-RRGP-CuttingTheTwinParadox-doppler-updated

Finally, you say

Interestingly, T appears to D to be traveling at 4 times the speed of light (i.e. - traveling 4 LY in 1 year of D's time). Of course, that's not what is actually happening.

The signal from event O (when and where clock-T reads 0) is received by clock-D when clock-D reads 4.

Clock-T meets clock-D when clock-T reads 3 and clock-D reads 5.

Of course, the velocity of clock T according to clock D is "4 LY / 5 Y", using the Minkowski-right-triangle with legs parallel to clock-D's diamonds and with hypotenuse OP'.

Your use of "appears" refers to "4LY" (the spatial-leg) and the segment between clock-D's 4th and 5th Y, which is not the usual rise-over-run.
By this logic, you would have to say that "a light ray appears to travel with infinite speed" since a light ray emitted at event O (by clock T) meets clock-D's at clock-D's 4th tick, before clock-T itself meets clock-D.
So, I don't think this is useful.
(It sounds provocative, but is likely to be misunderstood.)

I don't understand your last question.
But I don't think length-contraction is needed in any of these discussions.

robphy
  • 12,829
1

The key is that the synchronization method is only valid from S and D's point of view and not from T's point of view.

From S and D's point of view, the radio waves travel for 4 LY. Since they left x=0 at t=0, D should set their clock to 4 years.

But from T's point of view, the radio waves travel for only the Lorentz-contracted distance of 2.4 LY. So T believes that D should set their clock to 2.4 years.

From T's point of view, the clocks are not synchronized, and were never synchronized. It's analogous to flying across the US, leaving New York at 5pm and arriving in Los Angeles at 7pm. Did that flight take 2 hours? No, it took 5 hours because those clocks are, and always were, offset by 3 hours from one another. It's not meaningful to simply subtract those times unless T takes that offset into account.

Chris
  • 17,377