Why is a larger force needed when you decrease the distance in regards of torque?

Question

I think it's because of inertia.

Answer 1

I think OP is asking 'why when decreasing the distance from the rotation point of an object why is a larger force required in regards of torque?' Torque is defined as t=F*d where F is force and d is distance. If you want the torque to be constant and you decrease d then you need to increase F. If your question is why is torque defined as then that has been asked before for example here.

Edit: I believe this answer from the same link as I mentioned answers your question without math: "If you are rotating a body (applying a torque) you are doing work to rotate it over an angle. The same amount of work will be needed to cover that angle no matter what. At a greater distance from the axis the arc is larger, there is more distance to cover the same angle. So if the work required is the same but it is applied over a greater distance, you will need less force.

The moment arm affects the force in a torque because a larger moment arm, radius, or perpendicular distance means more distance to cover the same angle of rotation. " - BoddTaxter

Answer 2

In all cases work equals force times the distance over which the force acts, regardless of whether the distance is linear or over a circular path.

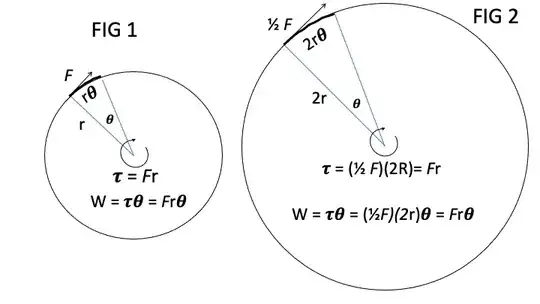
Rotational work equals torque times angular displacement in radians. See the figures below. Torque equals force perpendicular to the radius times the magnitude of the radius. Therefore the same torque and rotational work is achieved with a larger force and smaller radius as a smaller force and larger radius.

However, the smaller force, as shown in FIG 2 below, has to act over a longer circular distance to perform the same amount of work as the larger force, a shown in FIG 1, since the circular distance equals the radius times the angular displacement in radians.

Finally, regarding inertia, it is the property of an object, due to its mass, in which an object resists a change in linear or rotational motion motion ( change in its translational or rotational kinetic energy). From the work energy theorem the net translational or rotational work done on an object equals its change in translational or rotational kinetic energy. To go into that further, equations are needed.

Hope this helps.