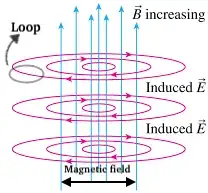
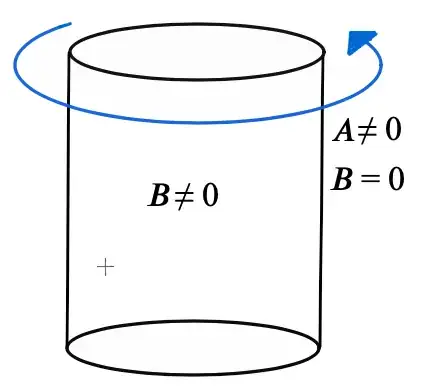
The difference in the radial dependence is the reason.
Circulation over any loop $\gamma$
$$
\oint_{\gamma} \mathbf E \cdot d\mathbf x
$$
can be expressed as integral over any surface $\Sigma$ whose boundary is the loop $\gamma$:
$$
\oint_{\Sigma} \nabla \times \mathbf E \cdot d\boldsymbol \Sigma,
$$
where $\nabla \times \mathbf E$ is called curl, and is a vector whose direction is perpendicular to plane in which circulation per unit area is the greatest, and length is circulation per unit area.
Let there be a cartesian coordinate system oriented in such a way that z axis is in direction of magnetic field, and electric field lines lie in the xy plane.
This curl can be calculated in cartesian coordinates using the standard method:
$$
(\nabla\times\mathbf E)_x = \partial_z E_y - \partial_y E_z,
$$
$$
(\nabla\times\mathbf E)_y = \partial_z E_x - \partial_x E_z,
$$
$$
(\nabla\times\mathbf E)_z = \partial_x E_y - \partial_y E_x.
$$
Let the loop lie in xy plane. Then curl in that plane has only z component
$$
(\nabla\times\mathbf E)_z = \partial_x E_y - \partial_y E_x.
$$
Field components inside the solenoid (or cylindrical region with uniform magnetic field) can be expressed as
$$
\mathbf E = Cr\mathbf e_{\varphi} = C(-y,x,0)
$$
with non-zero $C$ and thus z-component of curl of this field is
$$
\partial_x E_y - \partial_y E_x = C -(-C) = 2C.
$$
Thus any circulation integral in this region comes out nonzero.
For field outside the magnetic field, we have $\vec{E}=\frac{C}{r}\mathbf e_{\varphi}$, or
$$
\mathbf E = \frac{C}{r^2}(-y,x,0).
$$
When we calculate curl of this using the above rules, we get zero. Thus curl, that is circulation per unit area, is zero everywhere where field is given by the above formula. Thus circulation over any loop there comes out zero.