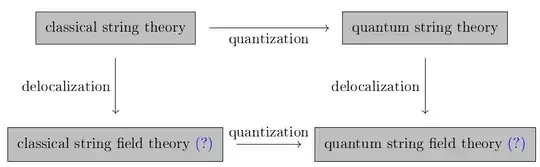
I am studying string theory and I realize that the relations between the different frameworks are not clear to me. Following this question, one could repeat the discussion but now taking $p=1$. We get a worldsheet, and a string that propagates in spacetime. I would now like to repeat the previous discussion but for strings.
The state of string is a point $(X^\mu(\tau,\sigma),\Pi^\mu(\tau,\sigma))$ in the phase space as before except that now position and momentum take two variables. We get what we could call the "classical mechanics of strings", or classical string theory (equivalent of relativistic classical mechanics but for strings). The worldvolume is now a worldsheet and can be provided with a Lorentzian metric. The interpretation of momentum and position as being field is now even easier, we call it the "worldsheet theory", it is $(1+1)$-dimensional.
We can now quantize the worldsheet theory. Position and momentum become operators and we get what we could call quantum string mechanics, but that we usually call string theory (equivalent of relativistic quantum mechanics but for strings).
Now, we are missing two corners of our square. Starting from classical string theory, we could "delocalize" (see previous question) and get classical string field theory. What would a classical string field be ? What kind of mathematical object ?
Furthermore, we could quantize this classical string field theory to get quantum string field theory, is that right ? Does this correspond to what people call string field theory (second quantization of the string)?
 $p=1$ square of frameworks" />
$p=1$ square of frameworks" />
In summary, I would like to clarify the relation between all those frameworks. This would also allow us to understand when we create "point particle-like" (QFT) excitations, "string-like" excitations (string field theory).