Why does the light passing through a prism get bent in the same direction twice?

Question

Whenever I see a 2D drawing of dispersion occurring when light travels through a solid prism, I see the rays get bent downwards on entry and downwards on exit again. For example here: https://www.wikiwand.com/en/Dispersion_(optics)
To my understanding of optics when entering a medium with a higher optical density, the ray should get bent towards the normal of the surface, rotated CW and CCW when entering one with a lower IOR. However, the drawings suggest that it gets bent in the same direction upon entry and exit.

Answer 1

The normals in consideration for the incident and emergent rays are different.

For simplicity, take a monochromatic beam of light incident on a prism, as shown in this figure:

1. When light is incident on a medium with a higher index of refraction ($n$), it bends towards the normal.
2. When light is incident on a medium with a lower $n$ it bends away from the normal.

In reference to this figure, the incident ray should bend towards the normal, which would mean a clockwise rotation ($\phi_1 < \theta_1$)

And the ray within the prism would bend away from the new normal at the new interface, corresponding to another clockwise rotation. ($\phi_2 < \theta_2$)

For a beam of light, dispersion will cause different wavelengths of light to bend in different angles, but they will all bend in the same sense.

Hope this helps.

---

Image source.

Answer 2

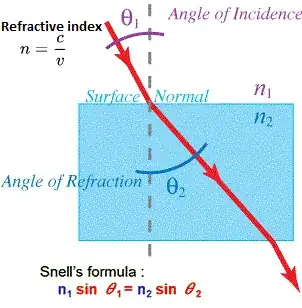
This is how refraction of light in a medium works.

The phase velocity $v$ of light changes transitioning from one medium to a different density medium according to its refraction index $n$ and the refraction angle to the incident is dictated by Snell's law:

Base image source: https://www.detailingwiki.org/detailing-miscellaneous/what-is-refractive-index/attachment/snellslaw1/

The light then exiting the medium and returning to the initial medium regains whatever phase velocity $v$ it had in this medium and therefore also to its initial incident angle.

If the boundary entry and exit surfaces of the medium are not parallel to each other, like the prism case, you have to algebraically add their difference to the exit angle. Snell's law does not change.