There is a lovely set of two-parameter spin chains that can be mapped to quadratic fermions and studied quite exactly:
$$H = -\sum_{i} \frac{1+\gamma}{2}\sigma^x_i\sigma^x_{i+1}+\frac{1-\gamma}{2}\sigma^y_i\sigma^y_{i+1} + h \sigma^z_i$$
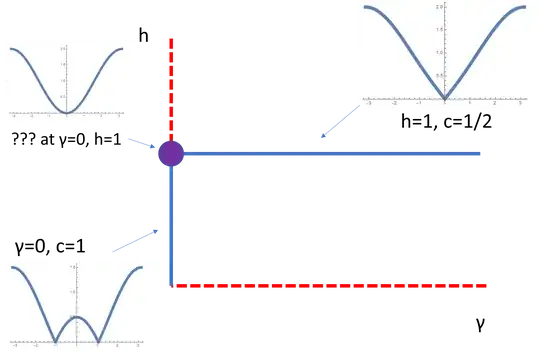
I'll consider $\gamma, h \geq 0$ in the following. These models show phase transitions with infinite correlation length on crossing the vertical line $\gamma=0, h<1$ and on crossing the horizontal line $h=1, \gamma>0$. In fact, these phase transitions flow to conformal field theories with a central charge that can be determined quite simply: on mapping to fermions, the central charge is half the number of points in the single particle spectrum with a linear dispersion relation.
Below, I plot $\gamma, h \geq 0$ with the critical lines where phase transitions occur. I also draw what the single-particle dispersion relation is after mapping to quadratic fermions. It's easy to see, using the rule above, that $c=1/2$ for the $h=1$ line and $c=1$ for the $\gamma=0, h<1$ line.
However, exactly at $\gamma=0, h=1$, there's a quadratic dispersion relation. My questions are: Does this critical point flow to a conformal field theory? If not, is there a general theory of what happens when one has two lines of fixed points intersect, with the lines each described by different central charges?
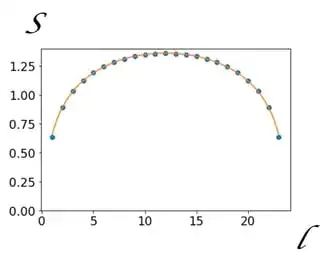
Using exact diagonalization on small system sizes, and barring any coding mistakes, I find this point's entanglement entropy to be well-described by a central charge of $1$, where I have fit $S(l)$ to the function $\frac{c}{3}\ln \left(\frac{L}{\pi} \sin{\frac{\pi l}{L} }\right) +C$
Numerically, the fit gives $1.04$, a good sign that despite the quadratic dispersion relation, properties of this model are determined by the $c=1$ fixed point of the rest of the $\gamma=0, h<1$ line.
EDIT: I accidentally dropped the factor of $1/2$ in $(1\pm\gamma)/2$ in the Hamiltonian above when making my above plot. When I correctly include the factor, I instead get an entanglement entropy of about $10^{-3}$ everywhere in the chain, which is really just zero, in line with both the excellent answers to this question noting product state ground states. It turns out that the vicinity of this multicritical point also has very surprising entanglement properties, as elaborated in comments to the answers.