Why isn't Magnetic force doing any work on the rod?

Question

Consider the situation given below :

The rod (of length $l$ and of some resistance "r") connecting the two rails is given a velocity $v$ in the direction shown. Now since this motion induces an emf in the rod, so a current flows in the close circuit. Now due to this current there is a magnetic force acting on the moving rod in the opposite direction of its motion which slows down the rod.

Now my teacher told me that the loss in kinetic energy appears in the form of joule heating only which is kind of unsatisfactory to me because the magnetic field is doing negative work on the rod (right ?) , so some of the kinetic energy of the rod should be stored in the magnetic fields too . When I asked this to my teacher he said MAGNETIC FORCES CAN'T DO WORK and nothing else which left me unsatisfied.

Can someone explain why isn't some of the energy being stored in the magnetic fields ?

Answer 1

The misconception here is that only the vertical component of the charge velocity and the horizontal component of the magnetic force are considered. Certainly, if you only look at the horizontal component of the magnetic force you will see this component does work, but the entire force does no net work. A nice mechanical analogy is a block moving up an incline. The components of the normal force do work on the block, but the normal force in its entirety does no work on the block because it is perpendicular to the velocity of the block.

The diagram above (not drawn to scale) shows how the magnetic force does no work on the charges in the rod. The charges have a velocity component along the rod (the current) as well as a component perpendicular to the rod (due to the charges actually moving with the rod). The magnetic force is perpendicular to the total velocity of the charges consistent with the Right Hand Rule, which in this case is up and to the left. The left component is the resistive force felt by the rod. The upward component you will find to be consistent with Lenz's law to oppose the change in magnetic flux through the current loop.

Since the magnetic force is perpendicular to the velocity of the charges, the magnetic force does no net work on the charges in the rod. This therefore means there is also no energy stored in the magnetic field.

Note that this analysis is done in the rest frame of the magnetic field as shown in the diagram (the rest of the wire loop is at rest here as well).

Answer 2

This debate is a bit of "much ado about nothing". The basis is as follows. If you look at the Lorentz force we see $$\vec F = q \vec E + q \vec v \times \vec B$$ which leads immediately to $$P = \vec F \cdot \vec v = q\vec E \cdot \vec v + (q \vec v \times \vec B) \cdot \vec v = q \vec E \cdot \vec v$$ So from the Lorentz force it seems that the B field does no work.

Similarly, if we look at Poynting's theorem we see: $$\frac{\partial u}{\partial t} + \nabla \cdot \vec S + \vec J \cdot \vec E = 0$$ where $u$ is the energy density of the EM field and $\vec S$ is the flux of EM field energy from one location to another. The only term that involves matter is $\vec J \cdot \vec E$, which is energy that is leaving the EM field and going into the matter, hence it is the work done on matter. So from Poynting's theorem it also seems that the B field does no work.

However, the reason that this is "much ado about nothing" is that the E and B fields are not independent of one another. While you can write the work as $\vec E \cdot \vec J$ we also have Maxwell's equations which describe relationships between $\vec E$ and $\vec J$ and $\vec B$, especially via Faraday's law and Ampere's law. $\vec E \cdot \vec J$ is a function of $\vec B$.

Suppose, in particular, that we wish to investigate further the specific claim:

the loss in kinetic energy appears in the form of joule heating only

The problem is that the term $\vec E \cdot \vec J$ includes all of the work done on the conductor. That is, it includes both the joule heating and also any other form of work done on matter. For instance, in a battery it will include joule heating and also chemical work increasing the chemical potential. Similarly, in a conductor it will include joule heating and also mechanical work.

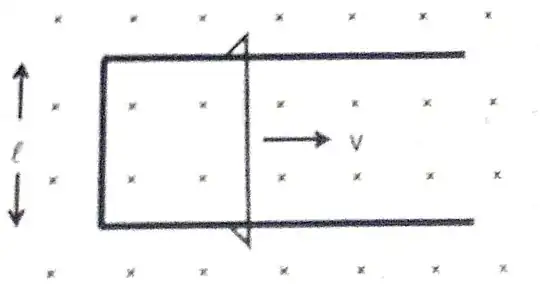
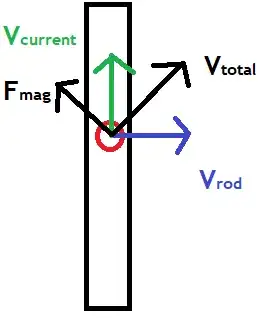
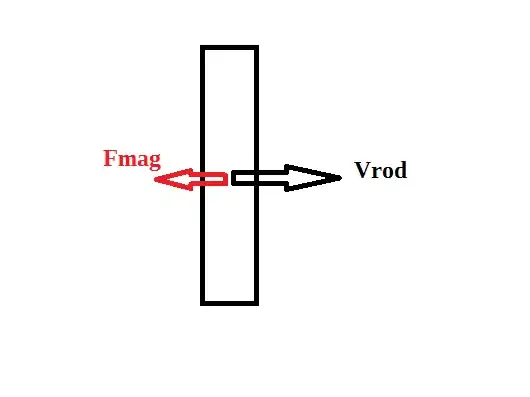
Let us make the assumption that in a conductor there is no other form of energy transfer besides joule heating and mechanical work. With that assumption, if the conductor is at rest then the mechanical work is 0 and $\vec E \cdot \vec J$ is indeed the Joule heating. However, in this case the conductor is not at rest. To determine the Joule heating we need to transform into the reference frame where the conductor is at rest.

Assuming that $v \ll c$ we have the following transformation equations where the primes represent quantities in the reference frame where the conductor is at rest:

$$\vec E' = \vec E + v \times \vec B$$ $$\vec J' = \vec J - \rho \vec v$$

Substituting those in we have: $$\vec E \cdot \vec J = (\vec E' - \vec v \times \vec B) \cdot (\vec J' + \rho \vec v)$$ $$=\vec E' \cdot \vec J' + \vec E' \cdot \rho \vec v - (\vec v \times \vec B) \cdot \vec J' - (\vec v \times \vec B) \cdot \rho \vec v$$ $$=\vec E' \cdot \vec J' + \rho \vec v \cdot (\vec E+ \vec v \times \vec B) - (\vec J-\rho \vec v) \cdot (\vec v \times \vec B)$$ $$=\vec E' \cdot \vec J' + \rho \vec v \cdot \vec E - \vec J \cdot (\vec v \times \vec B)$$

So finally we end with $$\vec E \cdot \vec J=\vec E' \cdot \vec J' + \vec v \cdot (\rho \vec E + \vec J \times \vec B)$$ which says that the total work $\vec E \cdot \vec J$ on a moving conductor is equal to the Joule heating $\vec E' \cdot \vec J'$ plus the mechanical work $\vec v \cdot (\rho \vec E + \vec J \times \vec B)$ where the mechanical work has the expected form which includes mechanical work done by the B field.

So while it is correct to say that $\vec E \cdot \vec J$ means that all of the work is due to the E field, it is also correct to say that $\vec E \cdot \vec J=\vec E' \cdot \vec J' + \vec v \cdot (\rho \vec E + \vec J \times \vec B)$ and therefore the B field does some mechanical work as expected. What is definitely incorrect to say is that the work is "in the form of joule heating only" because $\vec E \cdot \vec J$ is the total work and not only joule heating.

Answer 3

Consider what would happen to your rod without the application of an external force on the moving rod.
Due to the interaction of the current passing through the rod and the magnetic field there is a force on the rod to the left.
That force does negative work on the rod with the result that the kinetic energy of the rod would decrease.
There is no change in the strength of the external magnetic field acting on the rod and so there is no change to the energy stored in that external magnetic field.

To keep the rod moving at constant speed an external force must be applied to the rod to the right and then that external force will do positive work on the rod. An external force of just the right magnitude will result in no net work being done on the rod and so the rod will move at constant speed to the right.

The current in the rod is produced because of the interaction between the charges in the rod (all being made to move to the right) and the external magnetic field which has the effect of applying forces on the charges in the rod resulting in the mobile charge carriers moving along the rod (and around the rest of the complete circuit).
The forces on the charges in the rod are at right angles to the direction of motion of the rod and the direction of the external magnetic field.
This is the force on the charges in the rod (the magnetic force) which is at right angle to the direction of motion of the rod so in terms of that motion, the magnetic force does no work.

If the rod had no mobile charge carriers, ie was an insulator, then the steady state condition would be that the rod would have no force acting on it as there is no current passing though it, and the rod would move with a constant speed.

Answer 4

Οf course the magnetic field is doing work in your example and applying the magnetic Lorentz force on your moving target charges (force applied only to the segments in your drawing which are perpendicular to the magnetic field vectors).

(Notice, because the moving part of your conductive loop frame is elevated in relation from the rest of the frame as shown in your figure, your total frame is asymmetric and expect also a net torque to be applied to your frame).

This is a common misconception and wrong generalization about magnetic fields never doing any work, thus applying a force aligned to the motion direction and is true only for isolated charges (i.e. an electron inside a magnetic field, monopole electric field).

Because the magnetic force is always perpendicular to the motion of isolated charges, a static magnetic field cannot do work on an isolated charge. However, it can do work indirectly, via the electric potential dipole field generated in a conductor by a changing magnetic field. Magnetic field WP

In your case shown in your provided circuit diagram, the rod moving to the right and cutting the magnetic flux lines will change the magnetic flux in the area of the loop, thus a changing magnetic field inside the loop that will induce an electric field. The resulting vector field for the moving rod inside the magnetic field is shown below (right hand rule applied with the direction of the induced current in the conductor $I$ assumed to point upwards):

As shown above, the changing magnetic field is generated by initial mechanical force on the rod which starts to move to the right and cuts the magnetic flux of the static B field and increases the conductor (circuit) loop area. Thus a changing magnetic field inside the conductive loop, field B, that induces a current $I$, in the circuit thus the Lorentz force $F_\text{mag}$ is applied on the moving rod segment antiparallel to its velocity $V_\text{rod}$. Therefore, $F_\text{mag}$ is not vertical to $V_\text{rod}$ but antiparallel and the magnetic field via Faraday's induction is actually doing work here in this experiment. $F_\text{mag}$ is slowing down the velocity of the rod $V_\text{rod}$ to the right.

The electrons drift velocity inside the conductor rod is a few mm per hour so, $V_\text{current}$ therefore inside a conductor is practically zero and must be neglected $V_\text{rod}\gg V_\text{current}$. Drift velocity

So yes indirectly magnetic fields can do work on electric dipole field charges like that inside an electric current circuit but not on electric monopole field charges like that of an isolated electron.

For a more intuitive explanation about this conditional misconception "that "magnetic fields don't do work" cliche, please watch this 5 minutes video:

https://www.youtube.com/watch?v=1bXjB0zrjp0

There is a big difference of a free charge and a charge inside a conductor which can not move anywhere in space but is restricted inside the boundaries of the wire therefore has less-degrees of freedom in its movement.