0

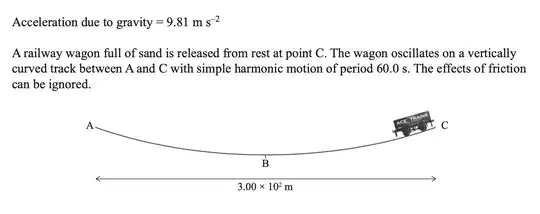
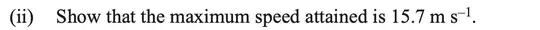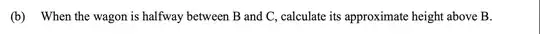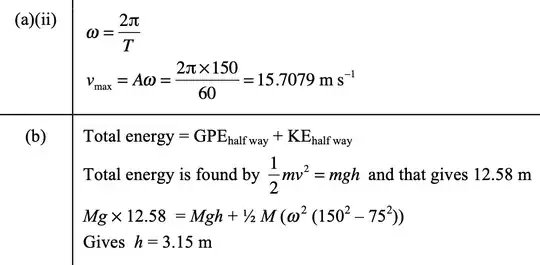This scenario is taken from the 2018 NZ Scholarship physics exam:

enter image description here

(Just in case the image doesn't load, it involves a wagon on a curved track (concave up). The wagon moves down from one side, to the other, then back again (with simple harmonic motion of period 60s). The question later goes onto say that the track is the arc of a circle.

The answers do not take this method, but I am wondering if it is possible to equate the motion of this wagon on this track, to the motion of some mass attached to a pendulum - that gives a SHM period of 60s, where the length of the pendulum is the radius of the circle this arc track is from. Is it possible to do so and why/why not?

The paper goes onto ask these 3 questions:

enter image description here enter image description here enter image description here

Solutions (without assuming this can be modelled with pendulum):

enter image description here enter image description here

We see the circle has a radius of 901m. However, if we assume it can be modelled by a pendulum, the radius / length of pendulum, will be 849m (found with $T = 2pi*sqrt(l/g)$. This suggests we cannot model this as a pendulum, why is this?

Qmechanic
  • 220,844
Jaynindu
  • 23

2 Answers2

1

If the track is a segment of a circle, the given setup is exactly equivalent to a regular pendulum on a string (sometimes called a mathematical pendulum when we ignore the mass of the string). The motion of the mass follows the exact same path, and the involved forces are equivalent. The only difference is that for a mass on a string, the force is provided by tension in the string pulling radially inward, while in this example it is provided by the rail tracks pushing, but also radially towards the center of the circle (since there is no friction).

Whether or not this can be treated as a harmonic oscillator depends on how large the amplitude is and how accurate the result should be. When solving a mathematical pendulum, we usually resort to approximating

$$ \sin{x} \approx x$$

for small values of $x$. Then the motion becomes a simple harmonic oscillation. If the amplitude is too large, this approximation doesn't hold very well.

noah
  • 10,404
  • 5
  • 29
  • 39
0

There is no reason this motion cannot be modeled as a simple pendulum (given meaningful data). In part (a)(ii) the 2π/T is the angular frequency of oscillation which is not the same as the maximum angular velocity. And, the given width tells you nothing about the radius. The given solution is nonsense.

R.W. Bird
  • 12,280