Time-dependent Magnetic Field "Paradox" with Faraday's Law

Question

I have encountered a "paradox" while studying electromagnetism and I can't seem to understand where I am messing up.

Consider a uniform, time-dependent magnetic field B(t) = $t^4 \hat{i}$ in some region of space.

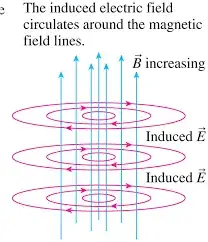
By Faraday's Law, there must be some induced electric field due to the changing magnetic field. However, since the magnetic field is uniform, any two points in the space are indistinguishable, so I believe that the electric field must also be uniform everywhere in that region of space. However, if the electric field at a point is independent of its position in space, then the E field must have curl 0.

So by Faraday's Law: $\nabla \times E = -dB/dt$. However, as per my above reasoning, the left side of this equation is 0 whereas the right side will be proportional to $t^3$? How can this be?

I have a few guesses as to where I went wrong, but no justification for why they should be true:

1. Maybe it is impossible to create a perfectly uniform magnetic field that increases with $t^4$? But if so, why would this be impossible?
2. Although the electric field is constant (at least per my reasoning) at any instantaneous moment, that constant value will change over time since the $E$ field is proportional to $t^3$. Maybe the time dependence of the $E$-field means something?

Answer 1

The left side of the equation will not be $0$. You are being misled by how symmetric the B field is.

One place you might expect to find a uniform time-dependent B field is inside a solenoid. This is a cylindrical region of space, with a current flowing around the cylinder. If you just think about how symmetric the B field is, you might expect no current could generate such a B field.

Likewise, the induced E field is cylindrical.

Picture from https://faculty.uml.edu//Andriy_Danylov/Teaching/documents/L18Ch33InducedEcovered.pdf

Answer 2

However, since the magnetic field is uniform, any two points in the space are indistinguishable, so I believe that the electric field must also be uniform everywhere in that region of space.

This is not so. Any two points are not indistinguishable just because they have the same magnetic field. They are still distinguishable in that they have different position in space.

In a realistic scenario, magnetic field can be made only approximately uniform in a finite region of space. Then the points of space differ in how far they are from the source of the magnetic field or from boundary of that region.

In purely hypothetical case of magnetic field uniform in the whole infinite space, we can only conclude that curl of electric field is uniform. But this does not in any way imply electric field is uniform; on the contrary, it can't be, because then curl would vanish, as you have realized.

Answer 3

A uniform magnetic field means that $\vec{B}(r,t)=\vec{cst}$ ,i.e $\frac{d\vec{B}(x,t)}{dt}=\vec{0}$