Yes, dark matter has to be in motion, otherwise it would fall in to the galactic center. From the fact that galaxies are stable, we can expect the Virial Theorem to hold, i.e. that dark matter has a total kinetic energy of half the total gravitational potential of the galaxy.
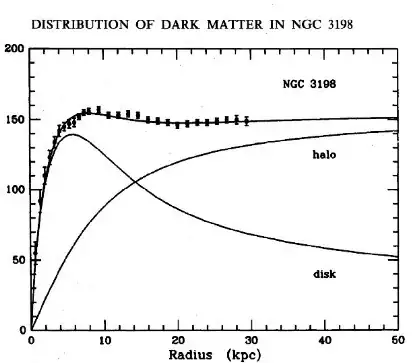
Yes, indeed, a particular density distribution is required to result in the observed rotation curve; taken the other way around, measurements of galactic rotation curves are measurements of the dark matter density profile. For simplicity (which turns out to be a good approximation) let's assume a spherically symmetric distribution and equate centripetal and gravitational forces:
\begin{equation}
\frac{mv^2}{r}= \frac{GM(r)m}{r^2}
\end{equation}
with $M(r)=\int \varrho(r) 4\pi r^2 \mathrm{d}r$ the dark matter mass profile. Sanity check: Outside the mass distribution, $M(r)$ can be approximated as a point mass $M$ at $r=0$ and one recovers Kepler's law $v(r)\propto 1/\sqrt{r}$, whereas close to the center, $\varrho(r)\sim const$ and thus $v(r)\propto r$. Good. Now, to get the observed flat rotation curve $v(r)=const$ requires $M(r)\propto r$. Such a mass distribution is what you get for a isothermal sphere, often used as the simplest example of a star in ASTR101 courses. A more detailed analysis and in particular a plethora of studies on intricate n-body simulations favors a modification to that profile called the Navarro–Frenk–White profile.
The take home message is that the dark matter velocity distribution is expected to roughly follow a thermal profile, i.e. a Maxwell-Boltzmann distribution. Modifications come from cropping that at the escape velocity, and from a decade-long debate whether the cores of galactic dark matter profiles are "cored" or "cusped". So, yes, our standard models of dark matter phase space distributions correctly reproduce the observed rotation curves of galaxies. Research is ongoing to investigate feedback mechanisms between the baryonic disk and the dark matter halo, and their impact on the observed distributions and scaling relations.
I can provide some pointers if you want, but to get an idea, have a look at the homepage of the Illustris collaboration. Every galaxy you see there is actually a simulated one, so we know the simulated dark matter profile and can compare this virtual universe to the real one to further our understanding of what is going on, despite not yet having detected dark matter quanta directly. The page also lists a number of papers with details for the so inclined. Or, if you prefer plots, from this first to find though somewhat dated paper comes this example of the velocity distribution in a simulated (dark matter-only) galaxy:
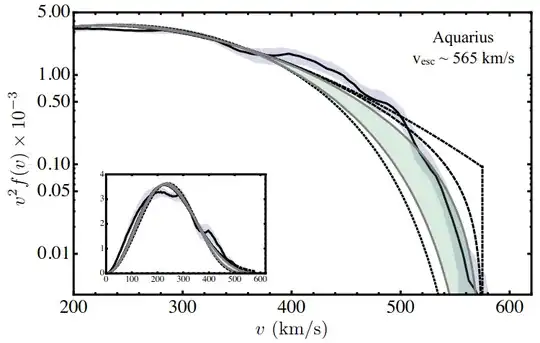
(Maxwell is dot-dashed, dashed and dotted other analytical models, solid black is the simulated profile. Green is what this particular paper propagates as a model, purple an idea about the spread seen in simulations. Also note the inset: as promised, the isothermal halo is a pretty good approximation.
Finally,
Have models been investigated for different motion e.g. where the dark
matter orbits at constant radius, or is stationary, or is even moving
at constant speed towards the galactic nucleus, to be periodically
ejected?
As mentioned dark matter can not be stationary in the galaxy's gravitational potential. The dark matter halo is not expected to condense into a disk, because (a) that would require efficient mechanism for dark matter to dissipate energy and (b) disk-only galaxies aren't stable as already some of the earliest n-body simulations confirmed. Yes, in the thermal halo, the individual dark matter quanta are expected to move on elliptical orbits. Ejection (of notable quantities) would mean evaporation of the dark matter halo which is in contrast to the observation that galaxies are around all the time (i.e. are stable)