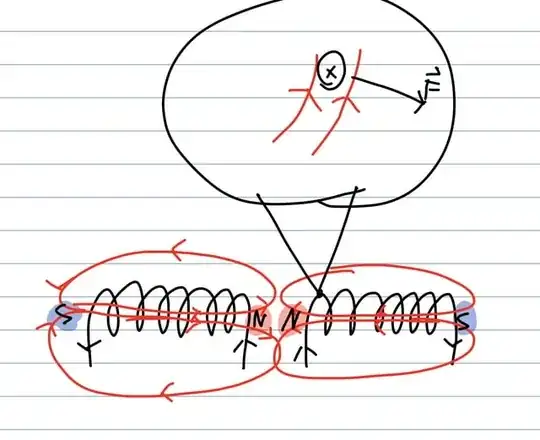
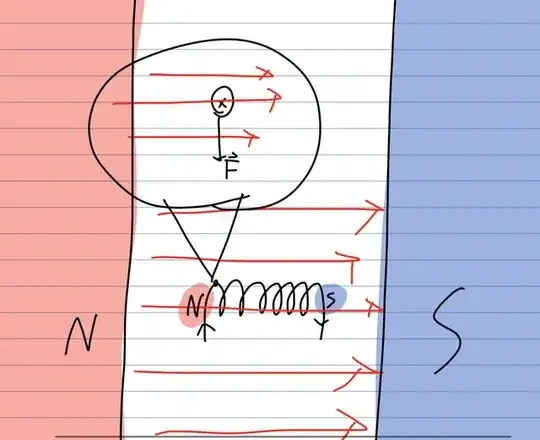
Basing this analysis off of the right hand rule I'm confused why the north pole of a solenoid would repel other north poles.
With two solenoids it kind of makes sense due to how the magnetic field curves at the poles.
However with a uniform magnetic field it doesn't make sense.
The right hand rule says that the force will simply point inwards.
In order to make computations simpler we can consider the solenoid to be akin to a perfect dipole with dipole moment $\vec\mu$ (this is a valid approximation if the dimensions of the solenoid are small and higher multipole terms can be ignored). Now the force due to a magnetic field on a dipole constructed out of a current loop is given as $$\vec F=\nabla (\vec\mu\cdot\vec B)$$ This can be derived from using the fact that the potential energy of a dipole in a magnetic field is $U=-\vec\mu\cdot\vec B$. From this, one can see that the force vanishes in a uniform $\vec B$. $$\begin{aligned}\vec F&=\nabla (\vec\mu\cdot\vec B) \\&=(\vec\mu\cdot\nabla)\vec B+\vec\mu\times(\nabla\times\vec B) \\&=0 \end{aligned}$$ Now the thing to keep in mind is that it is not possible to obtain a uniform $\vec B$ using any finite source. The best you can do is to approximate a uniform $\vec B$ in any experimental setup. This will result in non-uniform fields leading to small but non-zero forces on the dipole.
Imagine a solenoid is kept stationary, when you bring another solenoid (with like poles facing each other) the magnetic field is additive near the like poles which means net magnetic field increases in the region between them which implies the energy stored in magnetic field is increasing this energy comes from the work done by the agent who is bringing the solenoids together. This means that the forced applied by the solenoids is $F_{sol}=-\frac{\partial U}{\partial x}$ is negative or opposing the agent which tells us that the solenoid is pushing the solenoid away(repelling)
