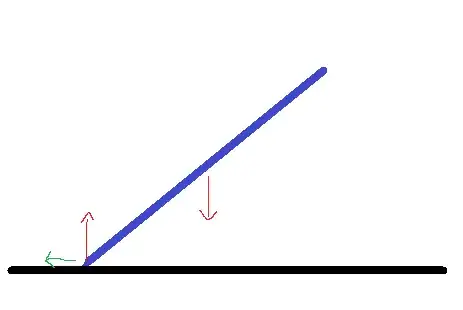
In the following picture, the blue bar represents a rod that is falling from the sky and the black line represents the ground. Hence, in the picture, the moment of the impact is shown. We assume the ground to be frictionless. Now, when time goes on, the rest of the rod will move towards the ground. However, while doing so, the rod will slide on the ground to the left (green arrow). At the contact point, there will be a normal force (red arrow). The gravitational force is also depcited by a red arrow.
Are the normal force and the gravitational force equal in magnitude and opposite (as indicated in the picture)? And where is the reaction force to the force acting in the direction of the green arrow?