Does the track do work? (second try)

Question

When a ball rolls without slipping down a track, it seems like static friction from the track does rotational work on the ball. As explained in this post: Is work done in rolling friction?, this work is exactly the same as the work done by gravity around the pivot point. But shouldn't the track also do linear (i.e. translational, not rotational) work on the ball? After all, the ball is moving.

(The fact that the pivot point is not moving does not seem to be a sufficient explanation because $F=ma$ holds and therefore so should the work-energy theorem for the displacement of the ball.)

Answer 1

But shouldn't the track also do linear (i.e. translational, not rotational) work on the ball? After all, the ball is moving.

when a block is sliding down a slope, the friction force $F$ does work and slows the block down. Work is done on the block because the force is acting parallel to the velocity.

For the ball, it's true that it's moving down the slope, $v_1$, but the point $P$ where the friction is acting is moving perpendicular to the force, in the direction of $v_3$.

The point $P$ moves in the shape of a cycloid, and moves perpendicular to the surface when in contact with it (e.g. at $2\pi a$)

The formula for work done is $W= Fd\cos\theta$, where $\theta$ is the angle between the force and the distance moved, so (ideally) no work is done on a rolling ball by friction.

Answer 2

This is a very (needlessly) confusing topic that, for whatever reason, is frequently taught incorrectly.

The power of a specific force is given by $P=\vec F \cdot \vec v$ where $\vec v$ is the velocity of the material at the point of application of $\vec F$. This simple definition works for any mechanical force in any classical mechanical scenario. Then the work done by that force is simply $W=\int P \ dt$.

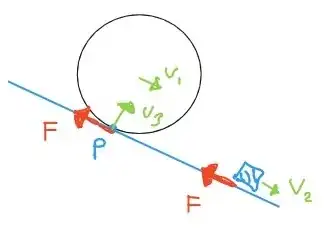
Now, specifically for this scenario, a ball rolling without slipping down an incline, there are three forces: the normal force, the frictional force, and the gravitational force.

The normal force and the frictional force are both applied at the contact point. The contact point is moving, but the velocity of the material at the contact point is 0. The contact point is not an object, so its motion is not important. What is important is the motion of the material at the contact point, which is $\vec v=0$. So then $P=0$ and $W=0$ for both the normal force and the frictional force.

The gravitational force, in contrast, is applied at the center of mass. The center of mass is moving at a nonzero $\vec v$ and $\vec F$ is not perpendicular, so $P=\vec F \cdot \vec v = F v \ \sin(\theta)$. So all of the work is done by gravity. The only source of kinetic energy, both linear and rotational, is the decreased PE from gravity.

Although the frictional force does provide torque it does not provide energy. That makes sense because the frictional force does not have an associated potential energy. The frictional force does convert some of the gravitational PE into rotational KE, but it does not do so by doing any work. The energy comes only from gravity.

This does not contradict the work energy theorem in any way. The net force is still related to the change in translational KE as specified by the theorem. The work energy theorem only tells you about the net force and the change in translational KE. It does not tell you anything about the work done by any individual force, even when there is only one force. Any attempt to use the work energy theorem to deduce the work done by an individual force is a misuse of the theorem.

Answer 3

Yes, the track does work. You can verify that the final velocity of the ball is less than $\sqrt{2gh}$. This is because the friction force did negative work.

This is exactly what is the work-energy theorem says: The sum of the forces on an object times the displacement of the center of mass of the object is equal to the change in $\frac12 mv^2$, where $v$ is the velocity of the center of mass of the object. This is precisely what is happening here. The static friction force acts against the motion of the ball and reduces its final linear kinetic energy.

As for conservation of energy, the work done by the friction force is exactly equal to the final rotational kinetic energy of the ball. The total change in kinetic energy (linear plus rotational) is indeed equal to $mgh$. So everyone goes home happy :).