I have been contemplating on how to solve for an $e$-field produced by a changing $b$-field, and when simplifying the differential equation, I ran into a problem where the integral form of Maxwell-Ampere's law does not describe physical reality - but instead gives us a mathematical model to describe what happens to a circuit loop under a changing $b$-field. The problem is, what if I want to actually understand the real $e$-field at every point due to a changing $b$-field? I don't have an interest in knowing the sum total of the $e$-field along an arbitrary loop.
$\nabla\times E = - \frac {\partial B} {\partial t}$
Wouldn't the curl of $E$ of an infinitely wide and uniform $b$-field be zero?
If so, then how would a loop inside the $b$-field have an induced voltage?
Basically, I've been beaten over the head with the integral forms of Maxwell's equations, which only serve some real world practical problems, but cannot fully explain what is actually occurring the reality.
Am I wrong in believing this?
Edit 1:
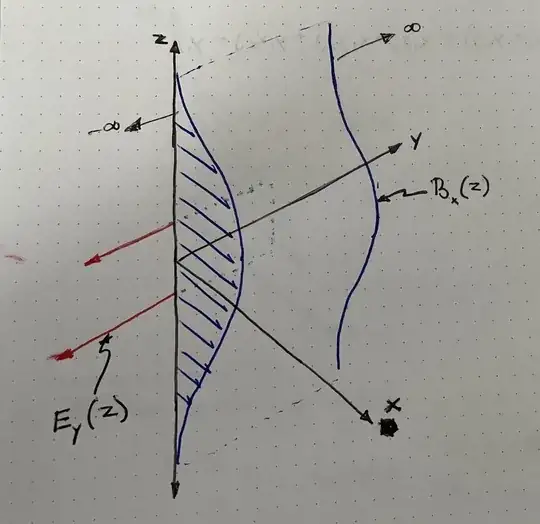
Suppose we have a dynamic b-field that points in the x direction. It only varies in the z direction.
$\nabla\times E = - \frac {\partial B} {\partial t}$
$\frac {\partial E_y} {\partial z} + \frac {\partial E_z} {\partial y} = - \frac {\partial B_x} {\partial t} $
$\partial E_y\partial y + \partial E_z \partial z = - \frac {\partial B_x} {\partial t} \partial z \partial y $
$E_z = 0 \leftarrow$ intuition tells me this, I don't see how it could have a value. Maybe this is incorrect.
$\partial E_y\partial y = - \frac {\partial B_x} {\partial t} \partial z \partial y $
$\partial E_y = - \frac {\partial B_x} {\partial t} \partial z $
in finite form
$\Delta E_y = - \frac {\partial B_x} {\partial t} \Delta z$
We can see how knowing $\Delta E$ can be beneficial for a circuit loop. After all, the driver in a circuit is potential difference or the $\Delta V$ - which is $\Delta E \cdot L$ but this doesn't help us much outside of circuits. How would I know the absolute value of E, rather than its relative value?
I know this question deviates a little from my original one, but I think it's strongly related. Pointing me to any resources will be helpful.