I was reading David J. Griffiths Introduction to Electrodynamics and came across this question today.

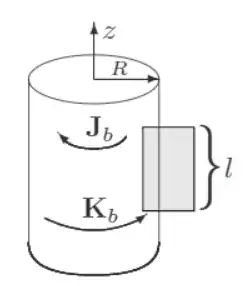
Part (b) of the question can be solved by realising that $\mathbf{H}$ (the auxiliary field), by symmetry, only points in the $\hat{z}$ direction.
Since $$\oint \mathbf{H} \cdot d\mathbf{s}=I_{enc,f}$$ and there is no free current in this case, $\mathbf{H}$ must be $0$, which then allow us to find the magnetic field, $\mathbf{B}$ through $$\mathbf{H}=\frac{\mathbf{B}}{\mu_0}-\mathbf{M}$$
Initially, the solution made sense to me. However, in the following section of the book which explains why we cannot always use Ampere's Law methods to find $\mathbf{H}$, it says
consider the example of the bar magnet—a short cylinder of iron that carries a permanent uniform magnetization $\mathbf{M}$ parallel to its axis. In this case there is no free current anywhere, and a naïve application of $\oint \mathbf{H} \cdot d\mathbf{s}=I_{enc,f}$ might lead you to suppose that $\mathbf{H}=0$, and hence that $\mathbf{B}=\mu_0 \mathbf{M}$ inside the magnet and $\mathbf{B}=0$ outside, which is nonsense. It is quite true that the curl of $\mathbf{H}$ vanishes everywhere, but the divergence does not. (Can you see where $\nabla \cdot \mathbf{M} \neq 0$?) Advice: When you are asked to find $\mathbf{B}$ or $\mathbf{H}$ in a problem involving magnetic materials, first look for symmetry. If the problem exhibits cylindrical, plane, solenoidal, or toroidal symmetry, then you can get $\mathbf{H}$ directly from $\oint \mathbf{H} \cdot d\mathbf{s}=I_{enc,f}$ by the usual Ampère’s law methods. (Evidently, in such cases $\nabla \cdot \mathbf{M}$ is automatically zero, since the free current alone determines the answer.)
I got quite confused after reading this and have a few questions:
What is the difference in the $\mathbf{H}$ and $\mathbf{B}$ field between a short cylinder and a infinitely long one?
Even though both scenarios exhibit cylindrical symmetry, why can we only use Ampere's Law method to calculate $\mathbf{H}$ for the case of an infinitely long cylinder?
Moreover, for Problem 6.12, $\nabla \cdot \mathbf{M}$ is not $0$ at the boundary of the cylinder. However, the book says that in cases where we can obtain $\mathbf{H}$ directly from Ampere's methods, $\nabla \cdot \mathbf{M}$ is automatically zero, since the free current alone determines the answer. What is the reason for this contradition? If $\nabla \cdot \mathbf{M}$ is indeed $0$ everywhere (including at the boundary), please explain why.
In conclusion, I am very confused by the book's explanation and have trouble identifying when we can use Ampere's Law method to find $\mathbf{H}$ field and when it is incorrect to do so.
Help would be much appreciated.