How does the double slit experiment ensure phase coherence?

Question

I am quite unsure of how phase coherence is ensured in the double slit experiment. The most typical answer that I have found is that the path length difference between the lights going in either double slit is zero, and so the phase is coherent. However, if we consider Young's experiment he used sunlight as his source which is incoherent. So in his setup, even though the diffracted light from the single slit pass through the same path length to reach the double slit, wouldn't the light still be incoherent?

I have seen explanations to this pointing out that the single slit acts as a point source for light and produces phase coherent light. If this is true, how can this be when the sunlight reaching the single slit is out of phase?

Answer 1

I am a fan of Richard Feynman and he used his path integral theory to explain much about light. He stated that every photon determines its own path .... and the corollary being that a photon will not travel a path if it cannot determine a path. The ideal path, the one of highest probability, is one that has an integer number of wavelengths, i.e. the distance between excited atom 1 and receiving atom 2 is ideally (or actually close to) this length, .... its all about probability.

How a photon determines a path is the result of transmission of forces (virtual photons) .... and real photons that transfer energy in/thru the EM field. It is the actual tight geometry of the DSE (narrow slits, pinpoint source, smooth screen) that only offers limited paths. Many photons approaching the first slit are actually reflected away ... just like hitting a mirror. The ones that pass satisfy the path integral and make the pattern.

The old classical interpretation is that photons must be in phase to cancel ... but photons never cancel as it would be a violation of conservation of energy. The classical and path integral theories have a lot of similarities mathematically and thus the classical theory is still taught today .... but you could argue its wrong to call it an "interference" pattern.

Answer 2

To understand why Young was able to realize his experiment with sunlight, we first need to understand a little bit more about the sunlight.

To say that sunlight is incoherent is the same to say that it has a low degree of coherence, but how much? And what kind of coherence measure we are talking about?

When we have a point source, any two points in its front waves, no matter how distant, could produce interference when averaged over time.

But we how there are no point sources in nature, just approximately dimensionless in some cases. It means that different points over the source will produce different wave fronts, not necessarily in phase with other points. The resultant profile of the wave front will not necessarily be all regular. The distance between two points in the wave front that could produce interference defines a diameter used to estimate the coherence area. We can use this measure to say how much the sunlight is coherent.

We should be aware about it to do an interference experiment, since our first slit width should not be greater than the diameter of the coherence area in order to observe diffraction from it. If the conditions of the experiment matches the coherence area previous mentioned, we can say that our light is coherent, at least for this experiment.

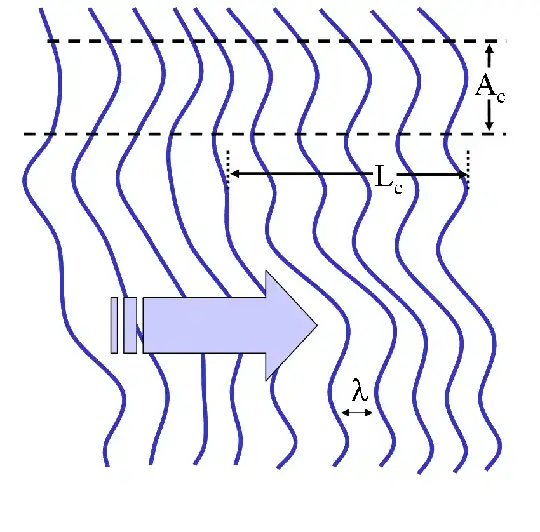
In this article we find the following formula for the coherence area

$$ A_c = {\lambda^2D^2\over A_S} $$

where $D$ is the distance from the source, $\lambda$ is the wave length and $A_S$ is the area surface of the souce. For the Sun, considering that for visible light we have $\lambda \propto 10^{-6} m$ and $D\propto 10^{11} m$ and $A_S \propto 10^{18} m^2$, we get $A_c\propto 10^{-8} m^2$. So the slit should have a width at most $10^{-4} m = 0.1 mm$, with matches in order of magnitude the slit width usually considered in this experiment (I searched for the Young's original data, but apparently he didn't mention the quantitative details of his experiments in his documented lectures).

After the sunlight passes the first slit, it will behave approximately like a pointwise source and we can place the two slits a little bit farther than previous calculated diameter, since know the coherence area will be greater.

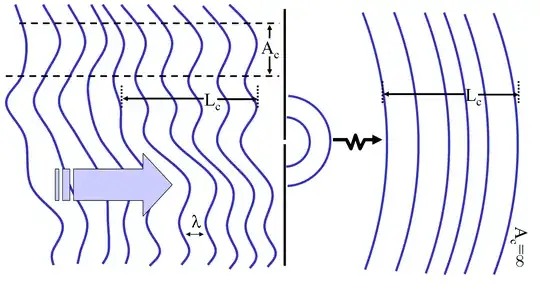
The only thing Young was not able to eliminate is the frequency length $\Delta \omega$ of the sunlight, which produced many superposed interference patterns for each different frequency. In this video, the YouTuber Veritasium made the Young's experiment with a box and test it by himself, and you can see how the pattern looks like.

The images was created by J S Lundeen and posted in English-language Wikipedia, in the aforementioned article. I just copied them here for convenience.