$n+n \rightarrow n+n$ scattering through photon interaction (QED Process)

Question

If I think about the quark level process then, two u quarks can scatter through photon exchange via QED interaction by following tree-level process

.

This is happening because u quark is electrically charged particle, which has a non-trivial charge under $\mathcal{u}(1)_{em}$, and then 2 d spectator quarks confined with u quark can form a hadronic bound state of the neutron.

On the other hand, if we think about the hadron level process, then as the neutron is an electric charge-neutral particle, it should not participate in QED interactions. Then the neutron should not be scattered through photon exchange. Then where is the ambiguity between my two arguments about quark level and hadron level thinking?

Answer 1

The paradox refers to low energies, where the neutron can be modeled as an elementary particle with zero electric charge. To resolve the paradox, remember that the neutron has a nonzero magnetic dipole moment. One observable effect of the neutron's magnetic dipole moment — at energies where the neutron can be treated as an elementary particle — is nicely reviewed in this answer by ACuriousMind. Regarding how much the magnetic dipole moment affects scattering, reference 1 says this on page 2:

The magnitude of the cross-section of the neutron magnetic scattering is similar to the cross-section of nuclear scattering by short-range nuclear forces.

In that paper, neutrons are used to probe the structure of condensed matter. That's a little different than pure neutron-neutron scattering, but it still illustrates the fact that the neutron's nonzero magnetic moment can have a non-negligible effect on scattering in general. Note that direct measurements of isolated neutron-neutron scattering are difficult: according to reference 2, direct measurements had still not yet been done as of 2005. For an update, see reference 3. But theoretically, the QED-mediated interaction does contribute, even at low energies where the neutron can be treated as an elementary particle. This resolves the paradox.

I said that the paradox only refers to low energies because at high enough energies, treating the neutron as an elementary particle is clearly not a good approximation any more: scattering — including QED-mediated scattering — can produce resonances or even break the neutron apart (into other hadrons, because quarks are confined).

---

References:

1. Zaliznyak and Lee (2004), Magnetic neutron scattering (https://www.bnl.gov/isd/documents/27263.pdf)

2. Mitchell et al (2005), A Direct Measurement of the Neutron-Neutron Scattering Length (https://www.scielo.br/j/bjp/a/kQFQgdY8CdC8wfg9F7dJXJt/?lang=en)

3. Stephenson et al (2012), Experiment on direct nn scattering — The radiation-induced outgassing complication (https://ui.adsabs.harvard.edu/abs/2012NuPhA.895...33S/abstract)

Answer 2

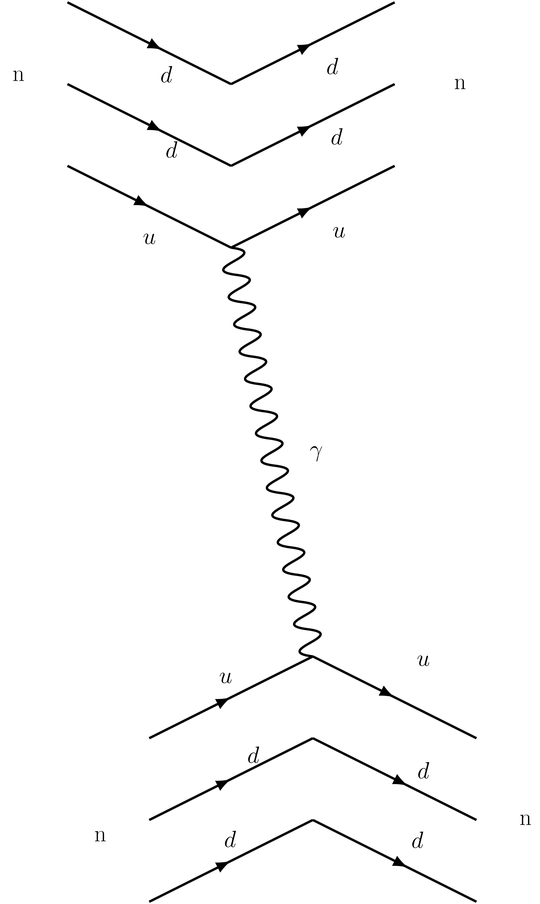
My sense is you know that the neutron is a composite particle of size 0.8 fm, and wonder how a tree photon interaction by anything charged inside the "upper" n (it's actually simpler to think of e-n scattering) can "see" the quarks of the lower n, but fail to "see" the whole as a neutral object.

The point is that for energies much lower than 1/(0.8fm) you see the total, aggregate charge of the n, null, because you must add the lowest-order tree diagrams you wrote, in this case the photon coupling to the u, plus to the d, plus to the other d valence quark. The resulting coupling, if you cannot resolve the difference among these three valence quarks, is just (2/3-1/3-1/3)=0! (This is something like the chiral bag model.)

The comments and the other answer remind you that if, at slightly higher energies, comparable to the inverse Compton wavelength of the n, you can resolve the three valence quarks, (they have a peculiar spin structure, where they contribute unequally), you can "see" their magnetic effects and the neutral n has a nontrivial magnetic moment, about -2/3 that of the charged proton! (This is because magnetism is shorter-ranged than electric forces.)

In fact, as you increase your scattering energy to come close to the above-mentioned radius of the n, you start seeing inhomogeneities in the charge distribution inside this neutral particle! The charge-radius-squared of the neutron is -0.1 fm², which, of course, means the negatively-charged d quarks are radially distributed "further out" in the neutron compared to the u quark", so to speak. The corresponding quantity for the proton is 0.6 fm². So for such higher energies, you indeed have a mismatch between the hadron and quark pictures: that's why people bother with the latter...