It looks like as if there was a race between our point running away from those galaxies (with the expansion of universe and space) and the light that was emitted at that time. And only now that light has reached and overtaken us.
That's correct. A photon from a distant source has to overcome the expansion of the universe in order to reach us. I'll illustrate it with an example. The graph below shows the path of a photon in an expanding universe (based on the Standard Model of cosmology and the latest data).
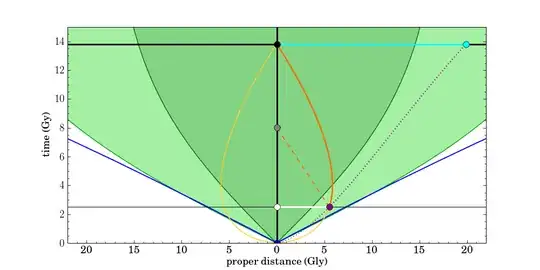
The horizontal axis shows the distance to us, and the vertical axis is the cosmic time. Over time, our galaxy moves on the black vertical line, and we're currently located at the black dot: the current age of the universe is 13.8 billion years.
Suppose that we're now observing photons from a distant galaxy. The redshift of those photons allow us to calculate when they were emitted, what the distance of the galaxy was at that time, and what the present-day distance of the galaxy is. In the graph, the galaxy emitted the light when the universe was 2.5 billion years old. The galaxy was located at the purple dot, while our own galaxy was at the white dot, and the distance between both was 5.52 billion lightyears (white line).
Now, if the universe wouldn't be expanding, then the light would've only needed 5.52 billion years to reach us (moving on the dashed orange line). However, the universe does expand, and as a result the light followed the thick orange line, taking 11.3 billion years to reach us. So because of the expansion of the universe, the light needed about twice as much time to reach us. During that time, the expansion caused the source itself to recede from us, following the dotted purple line, and its current distance to us has increased to 19.89 billion lightyears (cyan line).
There's one more interesting point: the source galaxy is receding from us faster then the speed of light (yes, that's allowed in General Relativity). Because of that, the distance between us and the photons was initially increasing (the expansion was 'winning' the race). But gradually the photons moved through regions that were receding from us slower: the dark green line represents the so-called Hubble distance: the region of space that is receding from us at the speed of light. So when the photons crossed that line, their distance to us began to decrease. All photons that we observe today have been travelling on this teardrop-shaped curve, which is called our past light cone.
But if that is so, then wouldn't it put a limit on the oldest light we can see, no matter how powerful the telescope is?
Yes. The maximum distance of regions of space that we can observe is called the cosmic particle horizon, and is shown in the graph as the thick blue line. You can think of it as the path of a photon sent out from our location at $t=0$.
If we zoom out the graph, it looks like this:
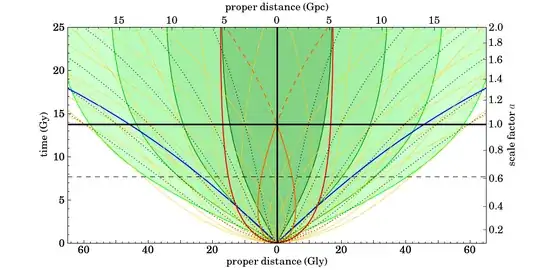
The current distance to the particle horizon is 46.2 billion lightyears, and everything inside it is called the observable universe. We cannot see anything beyond it.
This should be expected, because at the time just after the Big Bang, the light emitted by all objects must have already overtaken all other objects, including the location of earth.
No, in fact the expansion rate of the universe was very high in the beginning, so the photons from distant regions couldn't reach us. The expansion then slowed down, until it began to accelerate again when dark energy started to dominate (when the universe was around 7.7 billion years old).
If this is so, what is the theoretical limit we can see far back in the past?
In theory, all the way to the very early universe, when all particles were created (which, according to leading theories, was at the end of the inflation era). However, the early universe was so dense that it was opaque, so we cannot see photons from the first ~380,000 years (although in principle we could detect neutrinos from that era). When the universe was about 380,000 years old, the density was low enough for atoms to form, and photons could move freely. Those photons are the oldest light that we can see, forming the Cosmic Microwave Background.
For a more detailed and technical explanation, see this post.

