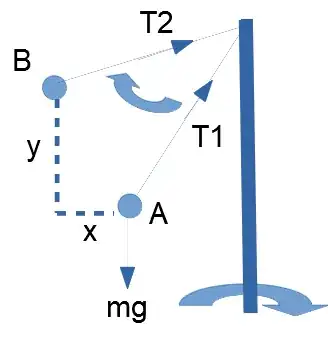
See image below:
Say I have a mass 'm' on a string or a very thin rod being twirled around on some pivot point by a motorised axle. Originally its twirling around in equilibrium in a horizontal plane at height A.
I then increase the rotational speed of the motor which will cause the 'string/thin rod' to rise up from height A to B .
I can understand how the increasing vertical component of tension T1 to T2 might cause the ball to rise height 'y' but I cannot understand the forces (if any ) that would move it 'x' and further away from the vertical spinning rod.
Am I missing something obvious?