I do know that for a perfect conductor, the electrical resistivity is zero at absolute zero temperature. But for an imperfect conductor (e.g. that we use in daily life) it is not zero even at $T=0^{\circ}K$ due to the presence of impurities, defects, edge effects, dislocations, discontinuation in the lattice structure etc. My question is how the electron interacts with each of these so that it’s motion is prohibited and we get some finite resistance even at absolute zero? I want to know the mechanism behind it in details.
Asked
Active
Viewed 1,312 times
2 Answers
5
In simple terms according to quantum mechanics a conductor which is perfect in terms of the regularity of the spacing of the lattice ions will have zero resistance.
Any deviation from perfection, eg impurities, dislocations, lattice vibrations (phonons) and edges, will influence the passage of the conduction electrons and hence introduce resistance.
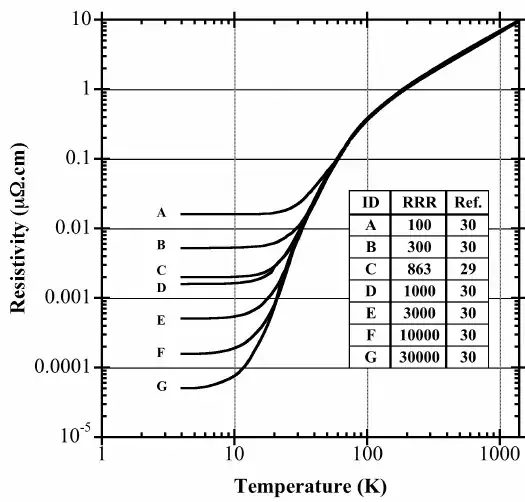
This graph of the resistivity of copper against temperature illustrates the idea with RRR being an abbreviation for Residual Resistance Ratio $= \dfrac{\rho_{\rm 300K}}{\rho_{\rm 0K}}$.
The drop in resistivity at higher temperatures is due to the reduction of the vibration modes of the entire material (lattice vibrations or phonons) and then the dislocations and impurities interactions with the conduction electrons become significant. As they become fewer, eg purer copper with fewer impurity atoms, single crystal sample etc, the residual resistance ratio increases. So sample $G$ is the closest to being perfect in terms of lattice regularity.
Farcher
- 104,498
2
The question is too broad to give a specific answer. I therefore outline the range of options, to enable the OP to specify the situation more clearly.
Resistance mechanisms
First of all, there exist multiple resistance mechanisms, not only the impurity scattering - such as phonon scattering, electron-electron scattering as well as scattering on dynamic impurities (such as magnetic impurities in certain alloys, where resistance diverges at low temperature due to the Kondo effect).
Localization
At very low temperatures, low electron concentrations, and low bias, one can indeed assume that the scattering is mostly due to static impurities. In this case the electrons have very long coherence length and one has to deal with effects of Anderson localization, which make material non-conducting, even though it is quasi-metallic in its origin (we usually deal with an n-doped semiconductor in this case, since in metals one cannot really neglect electron-electron scattering).
Quantum conductance
Even in absence of impurities the resistance is finite, as long as we are talking about a finit-size wire/conducting channel - see Ballistic conductance.
Roger V.
- 68,984