Why do we reduce only current to prevent power loss? Why not voltage?

Question

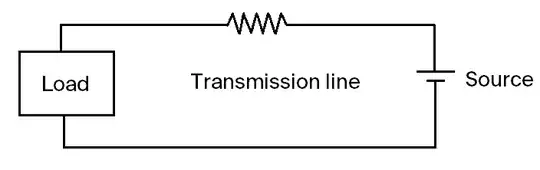
In power transmission lines current is kept low and voltage is kept high to reduce the power loss. This is because $P = I^{2}R$ and $P = VI$. In order to reduce power loss we have to reduce $I$ since $P = I^{2}R$ ($R$ is obviously a constant). And to reduce $I$ we have to increase $V$ because $P$ needs to be a constant ($P = VI$). Here's my question. Why don't we use the formula $P = \frac{V^{2}}{R}$? Now to reduce $P$ we have to reduce $V$. And to reduce $V$ we have to increase $I$ (since $P = VI$).

Answer 1

You need to pay attention to where the voltage is. Increasing the supply voltage does not mean that the voltage in all parts of the circuit go up. In fact, it might go down in some parts. Let's do a simple example. You need to supply a specified amount of power $P_{load}$ and you have a fixed distribution line with resistance $R_{line}$. However, you can choose the supply voltage $V_{supply}$ and the load will somehow cope (transformers or some other magic).

In these examples, I will use $P_{load} = 1MW$. The resistance of my line will be $R_{line} = 1 \Omega$ (round trip so each leg is $0.5 \Omega$).

Case 1 - lowish voltage distribution.

We aim to deliver $V_{load} = 1000V$ to the load. So, the load will need a current of $I = 1000A$ and the resistance of the load will need to be: $R_{load} = 1 \Omega$. The total resistance of the circuit will be $R_{total} = R_{line} + R_{load} = 2 \Omega$ and the supply voltage will need to be $V_{supply} = 2000V$. The voltage difference between the two ends of one distribution wire would be $500V$. So, the power loss in the line is $P_{loss} = I^2 R_{line} = 1MW$. We are losing as much in the line as the load. A terribly inefficient $50 \%$.

Case 2 - high voltage distribution

We aim to deliver $V_{load} = 1MV$ to the load. So, the load will need a current of $I = 1A$ and the resistance of the load will need to be: $R_{load} = 1 M \Omega$. The total resistance of the circuit will be $R_{total} = R_{line} + R_{load} = 1000001 \Omega$ and the supply voltage will need to be $V_{supply} = 1000001V$. The voltage difference between the two ends of one distribution wire would be $0.5V$. So, the power loss in the line is $P_{loss} = I^2 R_{line} = 1W$. So, boosting the voltage by a factor of $1000$ has not just reduced the loss by factor $1000$ but by factor $1000^2$ (million) and it is now negligible.

What is wrong with using the formula $P = \frac{V^2}{R}$? Nothing is wrong with it but you need to pay attention to the component that you are looking at. Note that I gave subscripts to $V$, $P$ and $R$ but not $I$. The reason is that the components are in series and so the current is the same in each. The resistance of the line is fixed but the load is not (see below). The voltage across the components varies as well.

Let's look at the load first. $P_{load} = \frac{V_{load}^2}{R_{load}}$ In case 1, $R_{load} = 1 \Omega$ and $V_{load} = 1000V$. Put these into the formula and you get $P_{load} = 1MW$. For case 2, different numbers go in but the same come out. This is not luck or coincidence; I chose $R_{load}$ to get this.

Now let's look at one wire of the distribution wires. Its resistance is $R_{wire} = 0.5 \Omega$. In case 1, the voltage between its ends is $V_{wire} = 500V$. $P = \frac{V^2}{R}$ gives $0.5MW$. There are two wires so the total power consumed by the wires is $1MW$ which is what I called $P_{loss}$. Doing this for case 2 gives a loss of just $1W$. This is the point of the exercise: by increasing the supply voltage, I need a lower current to deliver the same power. This means a lower voltage between the ends of the supply wires and less power lost in them.

Note that I needed to adjust the load between cases 1 and 2. I did not just boost the supply voltage with no change to the load; that would have a very different effect. Here is a simple but maybe not realistic example. My load is $1000$ resistive heating elements. Each is designed to receive $1000V$ and produce $1000W$. So, we can deduce that the intended current through them is $1A$ and the resistance is $1000 \Omega$. If I connect them all in parallel then they still need $1000V$ but the net resistance of the load will be $1 \Omega$, this is my case 1. Next I connect them in series, the net resistance will be $1000000 \Omega$ and I need to supply $1000000V$. This is my case 2.

I have ignored complications due to A/C effects and other factors e.g. leakage through insulation. A real life load will probably add many complexities but I hope that this gets the idea across.

Answer 2

What is throwing you, here, is the difference between the applied voltage and the voltage drop across the transmission line.

Consider a simple circuit, with a voltage source, a resistor, and a "device", in series. Here, the device plays the role of everything that is being powered through the transmission lines, the resistor plays the role of the transmission lines themselves, and the voltage source is the power station.

When discussing the power output by the power station, we have $P=V_pI_p$, where the subscript $p$ indicates that it's at the power station. The power loss through the transmission lines is $$P_l=V_tI_t=I_t^2R=\frac{V_t^2}R$$

However, by Kirchoff's Current Law, the current flowing from the power station is equal to the current flowing into the transmission lines. That is, $I_p=I_t$. On the other hand, we cannot say this about the voltage.

To determine the voltage drop across our transmission lines, we have to calculate it using Ohm's Law - that is, $V_t=I_tR$. And if we apply this calculation to $P_l=V_t^2/R$, we end up getting $P_l=I_t^2R$ back again.

---

We can imagine the scenario that switches the roles of $V$ and $I$ - suppose we were looking at a short-circuit situation. We have the voltage source, resistor, and "device" in parallel. In this situation, the voltage across the resistor and the "device" will be equal to the power source's produced voltage.

Then, to optimise power flow into the device, we want to maximise current and minimise voltage, as the power loss through the resistor will be proportional to the square of the voltage (as this is the "fixed" value).

Answer 3

There are two powers of concern here: the power dissipation of the transmission lines, and the delivered power. The delivered power is the whole point of the power lines in the first place. While reducing the voltage will of course reduce the power dissipation, it will also decrease the delivered power. What we are concerned with is not actually minimizing the power dissipation, but rather minimizing the ratio of the power dissipated to the power delivered.

The power dissipated by components of a circuit is proportional to effective resistance of that component, so we can increase the portion of the power that is consumed by our devices by increasing their effective resistance. And the thing about transformers is that when we step down the voltage, we increase the effective resistance of the devices on the stepped-down side. That is, if we step down the voltage by a factor of $10$, then a device in the stepped-down portion of the circuit with a resistance of $R$ will add $10R$ to the total effective resistance of the overall circuit.

Answer 4

We do reduce voltage. We reduce the voltage across the lossy part of the circuit, from one end to the other of each transmission line conductor itself, by reducing the current flowing through them.

However the purpose of the transmission line line is transmit power, so we maximise that by increasing the sending voltage between the two conductors as much as possible.

You have to pay attention to where the voltage is and why.

Answer 5

Let's start with a diagram that reasonably models an electrical system:

• The source converts mechanical/chemical/heat energy into electric voltage and current. The source has a finite power capacity (watts). But the voltage and current can be flexible, especially by using transformers.

• The transmission line is a pair of long copper/aluminum cables. It basically acts like a simple resistor. Because adding/changing cables takes a lot of effort, we can assume that this resistance is fixed.

• Generally speaking, the load has a certain desired power consumption. A house might consume 1000 W on average. Doubling the supply voltage will not entice the occupants to consume more power. If the voltage does change (e.g. America 120 V versus Europe 230 V), the load can compensate by using transformers, changing resistances of resistive devices, etc. to maintain a more-or-less constant power consumption.

Regarding the statements in your question, $P = I^R$, $P = VI$, and $P = \frac{V^2}{R}$ are all technically correct for each component. While every component experiences the same current, each component has a possibly different voltage and resistance, hence different power. So you need to analyze the power of each component separately.

---

A comparative example:

The load wants to consume 2 W. The transmission line has 1 Ω resistance. The source's potential is 5 V. How much power gets wasted?

$V_\text{source} = V_\text{load} + V_\text{line} = 5\text{ V}$. (Kirchhoff's voltage law)

$I_\text{source} = I_\text{load} = I_\text{line}$. (Kirchhoff's current law)

$P_\text{load} = V_\text{load}I_\text{load} = 2\text{ W}$. So $V_\text{load} = (2\text{ W}) / I_\text{load}$.

$V_\text{line} / I_\text{line} = 1\text{ Ω}$. So $V_\text{line} = I_\text{line} × (1\text{ Ω})$.

Substitute: $5\text{ V} = V_\text{load} + V_\text{line}$
$= (2\text{ W}) / I_\text{load} + I_\text{line} × (1\text{ Ω})$
$= (2\text{ W}) / I_\text{load} + I_\text{load} × (1\text{ Ω})$.

Multiply: $(2\text{ W}) + I_\text{load}^2 × (1\text{ Ω}) = (5\text{ V}) × I_\text{load}$.

Rearrange: $I_\text{load}^2 × (1\text{ Ω}) - I_\text{load} × (5\text{ V}) + (2\text{ W})= 0$.

Apply quadratic formula: $I_\text{load} = (5\text{ V} ± \sqrt{(-5\text{ V})^2 - 4(1\text{ Ω})(2\text{ W})}) / (2(1\text{ Ω}))$
$= (5\text{ V} ± \sqrt{25\text{ V}^2 - 4(1\text{ V}/\text{A})(2\text{ V}×\text{A})}) / (2\text{ Ω})$
$= (5\text{ V} ± \sqrt{25\text{ V}^2 - 8\text{ V}^2}) / (2\text{ Ω})$
$= (5\text{ V} ± \sqrt{17}\text{ V}) / (2\text{ V}/\text{A})$
$≈ (0.438\text{ or }4.562)\text{ A}$.

We will take the smaller solution because it wastes far less power in the transmission line. Finally, we have $P_\text{line} = I_\text{line}^2 R_\text{line} ≈ (0.438\text{ A})^2 (1\text{ Ω}) ≈ 0.192\text{ W}$.

Next, the load still wants to consume 2 W. The transmission still line has 1 Ω resistance. But the source's potential is 30 V. How much power gets wasted?

Going through the same derivation, we get $I_\text{load} ≈ 0.067\text{ A}$. Finally, we have $P_\text{line} = I_\text{line}^2 R_\text{line} ≈ (0.067\text{ A})^2 (1\text{ Ω}) ≈ 0.004\text{ W}$.

Answer 6

From the comments, this other question/answer answers your question, but I'll add a little more information.

It is the motion of electrons in the conductor that causes loss of energy during transmission, so if you were to use high current, low voltage for power transmission you would be maximizing the number of electrons moving and hence maximizing the amount of energy loss.

Using high voltage, low current means fewer electrons are moving (although they are moving with more force), and these fewer electrons dissipate less energy.

Answer 7

The physics behind the power loss is the interaction of the electrons carrying current with the material. This is why equations $P=I^2R$ and $P=V^2/R$, although normally mathematically equivalent, are not equivalent in physical grounds.

Moreover, one can imagine situations where there is finite voltage, but no current and hence no power loss. On the other case, if we have a current driven without voltage (e.g., due to inertia, when the conductor is accelerated), the power loss does happen.

Finally, on the microscopic level the concept of voltage is not applicable. Instead we have: $$w=\mathbf{j}\cdot\mathbf{E}, \mathbf{j}=\sigma\mathbf{E},$$ (where $\sigma$ could be a tensor.)

Answer 8

Why don't we use the formula P=RV^2

This gives you the power, not the power loss, as indicated by Andy Newman's comment. The power loss you want to minimize still is, unreplaceably, $I^{2}R$.