4

According to the perspective of a high school student,this question has been asked so pardon me for any lack of intuition or knowledge about this topic.

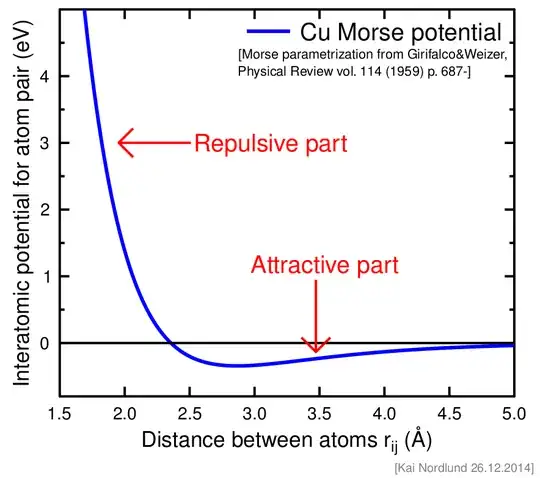
As far as I know as per Coulomb's law or Newton's law, attraction force or repulsion force should decrease as the distance increases between two particles(charged). When a spring is expanded, shouldn't its attraction force decrease as interparticular distance is increasing gradually? Then why does restoring force increase? I know this is an universal truth but I want to know why does this happen

Qmechanic
  • 220,844
MSKB
  • 624

3 Answers3

5

As far as I know as per Coulomb's law or Newton's law, attraction force or repulsion force should decrease as the distance increases between two particles(charged).

This is true; for example, because of electron distribution fluctuations, even neutral atoms are attracted to each other as $\sim r^{-6}$, where $r$ is the separation distance. However, they're also repelled more strongly (as $\sim r^{-12}$, say) at very close distances. The sum gives us a pair potential:

The sum of the two terms produces an energy minimum that corresponds to the equilibrium separation distance. And because every smooth minimum looks like a parabola up close, for small strain $\varepsilon$, the energy scales as $E\varepsilon^2/2$, where $E$ is a constant stiffness.

Thus, it's the balance between attraction and repulsion that causes the restoring force of springs to increase as we stretch them: although the attraction forces between molecules are lessening, the repulsive force is lessening more. Does this make sense?

Chemomechanics
  • 30,163
3

Newton's and Coulomb's laws apply to point particles interacting by gravitational and electrostatic forces only. That's far from the case in a solid, or even a diatomic molecule for which there are many interacting particles that are subject to Coulomb's law (Newton is negligible) and the laws of quantum mechanics. The situation of a diatomic molecule is complex; that of a solid considerably more so. When you pull the atoms of a diatomic molecule further from each other the complicated combination of Coulomb's law and quantum mechanics wants to bring them back together. There are some hand-waving classical pictures that demonstrate how a rearrangement of charges can "explain" the attraction, but they are very poor arguments. For starters (and finishers) they assume that atoms exist, but in classical physics atoms do not exist. The argument starts with a contradiction. The arguments also ignore the fact that the so-called exchange symmetry (roughly speaking, that's the Pauli exclusion principle) works to keep electrons apart ... in addition to the Coulomb repulsion. As I said earlier, the situation is complicated.

garyp
  • 22,633
3

The interatomic displacements are very small, since an elastically deformed body consists of zillions of atoms. Yet, for sufficiently big deformation Hooke's law breaks: first the deformation becomes non-linear, then plastic (i.e., the object does not return to its initial state anymore), and eventually it breaks.

Wikipedia figure of deformation stages

Roger V.
  • 68,984