String theory: why not use $n$-dimensional blocks/objects/branes?

Question

I have a basic question: if we use 1d string to replace 0d particle to gain insight of nature in string theory, and advanced to use 2d membranes, can we imagine that using $3$- or $n$-dimensional blocks/objects/branes as basic units in physics theory? Where is the end of this expansion?

Answer 1

There can not only, there have to be heavy higher dimensional objects (as for example D-branes) in string theory, as Joseph Polchinski discovered. So it is strictly speaking no longer appropriate to talk about "string theory", since M-theory is now known to relate all the different string theories known before by dualities and which contains these higher dimensional (from points D0, up to space filling D9 branes if spacetime is 10D) objects.

One way to see why these higher dimensional objects have to be there, is because T-duality transforms (among other things) the von Neuman boundary condition of a free floating open string, that are not stuck on anything, to the Dirichlet boundery condition which means that the endpoints are fixed. So there has to be something the strings can stick on, these objects are called D-branes which can be higher dimensional. That's the way Lenny Susskind introduced D-branes in this last lecture of his string course.

D-branes can for among other things be used to model the interactions of the standard model. For example QCD can be described by 3 D-branes, one for each color.

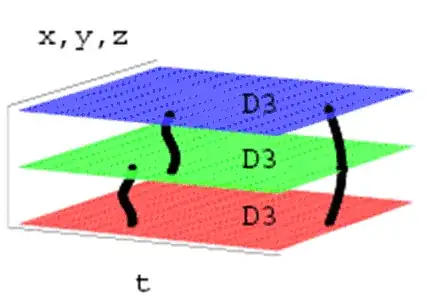
The mesons are strings which do not need to have both ends on the same "color" brane, quarks and anti-quarks are distinguished by the orientation of the string. Interactions take place when strings break and leave new end points on the brane and when two end points come together.

Answer 2

There are, actually. Dilaton already covered the reason through T-duality, so I will discuss the requirement of $p$-branes imposed by Ramond-Ramond potentials.

The worldsheet of a string can couple to a Neveu-Schwarz B-field: $$q\int_{}^{} {{{h^{ab}}}\frac{{\partial {X^\mu }}}{{\partial {\xi ^a}}}\frac{{\partial {X^\nu }}}{{\partial {\xi ^b}}}B_{\mu \nu }\sqrt { - \det {h_{ab}}} {{\text{d}}^2}\xi } $$

($q$ is the electric charge) The worldsheet of a string can couple to graviton field (spacetime metric): $$m\int_{}^{} {{{h^{ab}}}\frac{{\partial {X^\mu }}}{{\partial {\xi ^a}}}\frac{{\partial {X^\nu }}}{{\partial {\xi ^b}}}g_{\mu \nu }\sqrt { - \det {h_{ab}}} {{\text{d}}^2}\xi } $$

You can change the "$m$" to any form you like, in terms of the tension/Regge Slope parameter/string length etc.

For a dilaton field, $${q }\ell _P^2\int_{}^{} {\Phi R\sqrt { - \det {h_{\alpha \beta }}} {\text{ }}{{\text{d}}^2}\xi } $$ Ignore conformal invariance for the time being.

But what about Ramond-Ramond potentials? All is fine with the Ramond-Ramond fields, but the Ramond-Ramond potentials $C_k$are associated with the Ramond-Ramond field $A_{k+1}$ and it is clear that they can't couple similarly to the worldsheet. But it can couple to a higher dimensional worlvolume -- $${q_{{\text{RR}}}}\int_{}^{} {C_{{\mu _1}...{\mu _p}}^{p + 1}\frac{{\partial {x^{{\mu _1}}}}}{{\partial {\xi ^{{a_1}}}}}...\frac{{\partial {x^{{\mu _p}}}}}{{\partial {\xi ^{{a_p}}}}}{h^{{a_0}...{a_p}}}\sqrt { - \det {h^{{a_0}...{a_p}}}} {{\text{d}}^{p + 1}}\xi } $$

Which requires membranes and other higher-dimensional objects. It's interesting to note that while 10-dimensional string theories permit all sorts of these branes, M-theory only permits 2 and 5 dimensional branes.