3

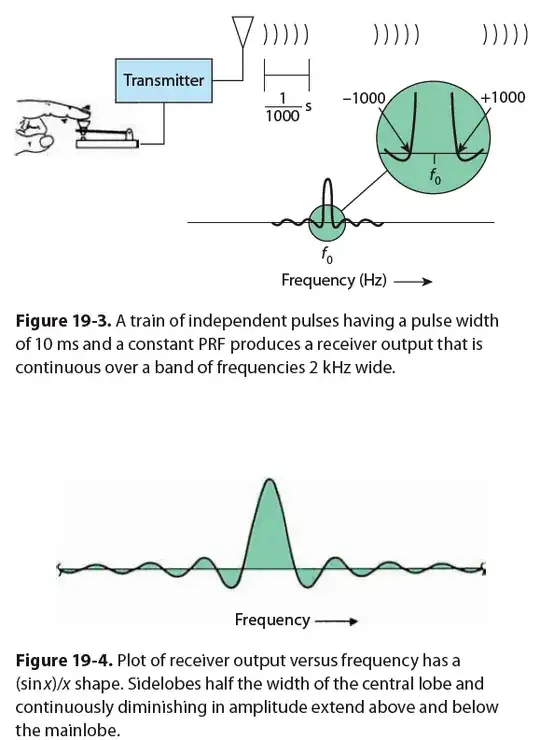
A continuous wave signal of 'f' kHz will appear on a receiver plot tuned in at f kHz and nothing else, ie it is 1 Hz wide. However, apparently this is not the case with pulsed signals and I'm struggling to understand why. Apparently, even if the transmitted pulses all have a consistent frequency, eg pulses containing a f kHz signal, and these pulses are transmitted at consistent intervals, the received signal does not appear as a narrow vertical line 1 Hz wide, but rather as a "band" with a main lobe, the centre of which would be our f kHz signal, extending to x kHz below and x kHz above it (the distance between the two being the pulse's bandwidth), and with a succession of higher and lower frequency lobes also extending out.

Pulsed signals and bandwidth

My textbook seems to be implying that the reason for this is because of the lower average power of a pulsed signal vis-a-vis a CW signal at the same frequency (because of the time that the transmitter is "off"):

Because of the signal’s lower average power (the transmitter is “on” only a fraction of the time, whereas before it was on all the time), the receiver output is not as strong as before, but it still occurs at the same point, $f_0$, on the dial. However, the plot of receiver output versus frequency is not quite as sharp as before. In fact, when expanded, it is continuous over a band of frequencies extending from 1 kHz below $f_0$ to 1 kHz above it. In other words, the null-to-null bandwidth is 2 kHz.

But I cannot understand why this would allow us to detect the original signal at 1 kHz above or below it (if this is indeed what it is suggesting).

Mark H
  • 25,556
VeryCommonName
  • 289

1 Answers1

6

A pulse has more bandwidth than a single frequency because a pulse has an amplitude envelope, and the envelope as you can imagine must contains other frequencies.

I'm trying to find you a better image, but at least in this animation you can see how the envelope [black] and the underlying CW signal with an envelope [red] have different frequencies (you can ignore the blue signal):

enter image description here

You can see that the underlying signal and the envelope are multiplied to produce the red plot above. Another way to look at it is that multiplication in the time domain produces addition* in the frequency domain. Therefore when you pulse a CW signal you must be adding frequencies which will by definition increase the bandwidth $^{1}$.

Especially you can appreciate the 'sharper' the edge of the pulse the more bandwidth it must have due to the greater number of harmonics required to produce a sharp edge.

We can see this kind of effect, for example when we observe the sum of fourier series to produce the sharp edges of a square wave as shown in this animation. Where each frame adds an harmonic, which begins to converge to an increasingly sharper edge [in red]:

enter image description here

The change in average power in your example doesn't really have a direct bearing on the reason that a pulse has more bandwidth than a single frequency. But rather is a consequence of the fact the transmitter is transmitting for less total time.

* Technically pairs but don't worry so much about that right now. Focus on this and come to that later imo.

$^{1}$ Quick caveat, assuming the new frequencies do not fall within the originally established bandwidth.

antimony
  • 208