Angular momentum conservation in collisions about point of impact

Question

We use the idea that if a body collides with something, its angular momentum is conserved concerning the point of impact. Source

It is clear to me that all impulsive forces and the colliding bodies' weight get cancelled off, but what about the weight of the body which gets hit?

In the above rod, when it is hit by a ball at any point initially when it is perfectly vertical, the statement is true, but as soon as it moves even a little, it is false. Hence, it doesn't seem right to me to say that angular momentum and after are the same.

Answer 1

The angular momentum is conserved when there is no net torque acting on the body. In this case, the weight of the body is providing a restoring torque, and hence the angular momentum is not conserved.

Answer 2

This question is the rotational dynamics equivalent of the query Can linear momentum be conserved before and after collision in the presence of an external force? but in this case it is the impulsive torque due to the gravitational force which is very much less than the impulsive torque due to the applied impulse.

Answer 3

What is CP and if you are asking L would be conserved or not it would be conserved just before and after the collision but not in the subsequent motion of the rod since weight of the rod will apply a net anticlockwise torque.

Answer 4

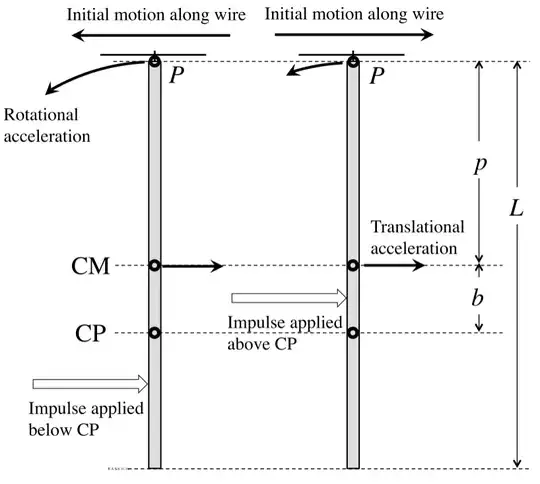
We use the idea that if a body collides with something, then its angular momentum is conserved with respect to the point of impact.

This is a direct result of Newton's 3rd law. During impact, there is an exchange of momentum between the bodies impacted. This exchange happens along a line called the axis of percussion defined by the momentum vector and the point of contact.

If you were to take the moment of momentum (torque of impulse) about this line the result would be zero. This is what this statement says.

A better way to describe the situation would be just to say the impulses exchange momentum between two bodies along a line in space. Or the corollary if an impulsive force has zero moment (angular momentum) about a point, then the action of the force goes through this point.

_{Also, since the impact happens at an infinitesimal time slice, only the impulse forces are considered as all other regular forces need a finite time interval to act.}

In the diagram below I have separated the bodies out to show Newton's 3rd law in action.

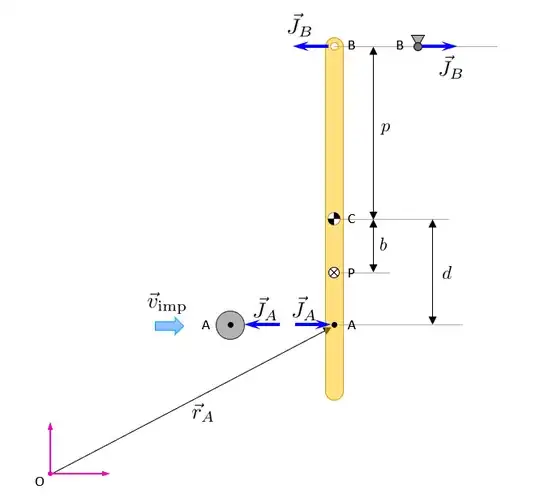
The impulse $\vec{J}_A$ acting on the impacted body (the hanging bar) at an arbitrary point A, has angular momentum about the origin of

$$ \vec{L}_O = \vec{r}_A \times \vec{J}_A $$

But if you sum up the angular momentum about the point of contact, then

$$ \vec{L}_A = 0 $$

What angular momentum really tells you is where the line of action of the impulse is in space.

An equal and opposite impulse $\vec{J}_A$ acts on the impacting body, which means that total momentum is conserved.

At the same time a reaction impulse $\vec{J}_B$ develops on the pivot, which again due to Newton's 3rd law keep the total momentum the same when considering the body and the earth as as system. Otherwise the reaction impulse $\vec{J}_B$ acts on the body changing the total momentum of the system.

The equations of motion describe the change in motion due to the impulses. In 2D these are

$$ \begin{aligned} J_A - J_B & = m \Delta v \\ d\,J_A + p\, J_B & = I \Delta \omega \\ \end{aligned}$$

But you also have the kinematics which state that

$$ \Delta v = p\, \Delta \omega$$

These have the solution of

$$\begin{aligned} \Delta \omega & = \tfrac{ d+p }{I + m p^2} J_A \\ J_B &= \tfrac{I - m\, d\, p}{I+m p^2} J_A \end{aligned} $$

You can immediately see that when $d = \frac{I}{m p}$ there is no reaction impulse, and we designate the point as the center of percussion $b = \frac{I}{m p} = \frac{\kappa^2}{p}$ where $\kappa$ is the radius of gyration of the object.