Centrifugal Force & Rotating Frames

Question

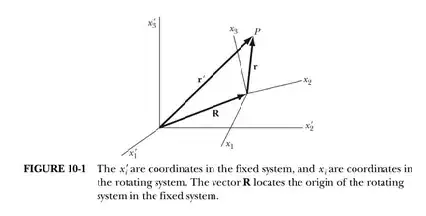
In Thornton & Marion's Classical Dynamics, the following relation is given for the rate of change of an objects position in the two coordinate systems (according to the picture shown at the bottom): $$ \bigg(\frac{\text{d}\vec{r}}{\text{d}t}\bigg)_{\text{fixed}} = \bigg(\frac{\text{d}\vec{r}}{\text{d}t}\bigg)_{\text{rotating}} + \vec{\omega} \times \vec{r}, $$ which, when applied to the coordinate change $ \vec{r}' = \vec{R} + \vec{r} $, yields the velocity relation $$ \bigg(\frac{\text{d}\vec{r}'}{\text{d}t}\bigg)_{\text{fixed}} = \bigg(\frac{\text{d}\vec{R}}{\text{d}t}\bigg)_{\text{fixed}} + \bigg(\frac{\text{d}\vec{r}}{\text{d}t}\bigg)_{\text{rotating}} + \vec{\omega} \times \vec{r}. $$ However, I this specification of fixed/rotating seems unnecessary, when all information regarding the transformation is encapsulated within $ \vec{r}'(t) = \vec{R}(t) + \vec{r}(t) $, with $ \vec{R}(t) = R(t)\hat{u}(t) $, provided that I correctly differentiate the changing unit vectors. Differentiating, applying Newton's 2nd law, I get what seems to be an almost correction derivation of fictitious forces, $$ \vec{F}'(t) = m \vec{a}(t) + m \frac{\text{d}\vec{\omega}(t)}{\text{d}t} \times \vec{R}(t) + m \frac{\text{d}^2 R(t)}{\text{d}t^2}\hat{u}(t) + 2 m \vec{\omega}(t) \times \vec{V}(t) + m \vec{\omega}(t) \times \big(\vec{\omega}(t) \times \vec{R}(t) \big) $$ with $ \vec{V}(t) = \hat{u}\cdot\text{d} R(t) / \text{d}t $, which is exactly correct in that this includes an Euler force, a linear acelleration term, a Coriolis term, and a centrifugal term... except that the Coriolis term provided by Marion points in the direction of $ \vec{\omega} \times \big( \text{d}\vec{r}/\text{d}t \big)_{\text{rotating}} $, rather than $ \vec{\omega} \times \vec{V} $! It depends on the velocity in the unprimed frame, rather than the velocity of the moving frame itself.

I can't find where my reasoning goes wrong, as my derivation all flows from the (seemingly true) fact that $$ \frac{\text{d}\vec{r}'(t)}{\text{d}t} = \frac{\text{d}\vec{r}(t)}{\text{d}t} + \frac{\text{d}\vec{R}(t)}{\text{d}t} = \frac{\text{d}\vec{r}(t)}{\text{d}t} + \frac{\text{d}R(t)}{\text{d}t}\hat{u}(t) + R(t) \frac{\text{d}\hat{u}(t)}{\text{d}t} = \frac{\text{d}\vec{r}(t)}{\text{d}t} + \vec{V}(t) + \vec{\omega}(t) \times \vec{R}(t) $$ I feel that my machinery is close. When the entirety of the information regarding the rotating and stationary frames is completely determined by the vector addition of position vectors, why on earth does one need to introduce this bizarre notation of fixed/rotating in the derivatives?

This is all to say, isn't the definition of $ \big( \text{d} \vec{r} / \text{d} t \big)_{fixed} $ literally the exact same thing as $\text{d}\vec{r}' / \text{d}t = \text{d} \big( \vec{R} + \vec{r} \big) / \text{d}t$? All information regarding rotation can be captured by $ \vec{R}(t) = R(t)\hat{u}(t) $ alone, so why introduce the parenthesis-frame notation?

Answer 1

To express the equation of motion in the non inertial system you have to take the first and second derivatives of position in the non inertial system. You relate the second derivative (acceleration) in the non inertial system to the second derivative in the inertial system to obtain the fictitious forces in the non inertial system.

I do not know of a valid approach that does not take the derivative in the non inertial system, since it is in that system where the fictitious forces arise.

If you consider the special case where $\vec R$ is zero- no translation of the non inertial system- but the non inertial system is rotating, I think your approach does not work. Specifically, for $\vec R$ of zero you have in your final paragraph using your notation ${{d \vec r^{'}} \over {dt}} = {{d (\vec R + \vec r)} \over {dt}} = {{d \vec r} \over {dt}}$ which is true since $\vec r^{'} = \vec r$ for $\vec R$ of zero. You are taking derivatives in the inertial frame, but you need to take the derivative of $\vec r$ (or equivalently $\vec r^{'}$) in the non inertial frame, since you want the motion in the non inertial frame (see first paragraph above). The time derivative of $\vec r$ (or equivalently $\vec r^{'}$) in the rotating (non inertial) frame is not equal to the time derivative of $\vec r$ (or equivalently $\vec r^{'}$) in the fixed (inertial frame). As discussed below $({{d \vec r} \over {dt}})_{fixed} = ({{d \vec r} \over {dt}})_{moving} + \vec \omega \times \vec r$ where $({{d \vec r} \over {dt}})_{moving}$ is the derivative in the moving system.

You need to use the correct relationship between the time derivatives of a vector in both the inertial and non inertial systems. Any (free) vector $\vec A$ is the same in both the fixed (inertial) and moving (non inertial) coordinate systems, considering both translational acceleration and rotation (with angular velocity $\vec \omega$ which may change with time) of the moving system relative to the fixed system. The components (e.g. Cartesian) and time derivatives of the vector are not the same in the two coordinate systems. It can be shown (even considering translation as well as rotation of the non inertial system) that the time derivatives of any (free) vector $\vec A$ relative to the moving and inertial coordinate systems are related by $({{d \vec A} \over {dt}})_{fixed} = ({{d \vec A} \over {dt}})_{moving} + \vec \omega \times \vec A$.

Since the Cartesian unit vector in the moving system $\vec i_{moving}$ is at rest in the moving system, $({{d \vec i_{moving}} \over {dt}})_{fixed} = \vec \omega \times \vec i_{moving}$, and so on for $\vec j_{moving}$ and $\vec k_{moving}$.

I believe your problem is that you are not correctly taking derivatives in the moving system.

Suggest you look at the text Mechanics by Symon; he considers the case of pure rotation (R of zero) and the case of translation as well as rotation. His text, though old, provides the clearest explanations and detailed derivations that I have seen.

Answer 2

I feel that my machinery is close. When the entirety of the information regarding the rotating and stationary frames is completely determined by the vector addition of position vectors, why on earth does one need to introduce this bizarre notation of fixed/rotating in the derivatives?

Your machinery is not close. What you are missing is a concept that Marion (and Goldstein, and many other texts) glosed over and instead choose to use a complete hand-wave. The concept is that there is a time-dependent transformation from the fixed frame to the inertial frame:

$$\vec r_I(t) = \mathbf T(t)\;\vec r_F(t)\tag1$$

Here, $\mathbf T(t)$ is a time-varying special orthogonal 3x3 matrix, $\vec r_F(t)$ is the position of some object in body-fixed coordinates, and $\vec r_I(t)$ is the position of that object in non-rotating (aka inertial) coordinates. In physics, we call things like $\mathbf T(t)$ transformation matrices or rotation matrices. I like to use the term "transformation matrix" as a matrix that transforms the representation of a vector from one frame to another. (I use "rotation matrix" to represent the physical rotation of an object without switching frames; e.g., rotating the hour and minute hands on a clock after the battery fails.) This is a transformation from one frame to another (inertial to fixed), hence $\mathbf T(t)$ rather than $\mathbf R(t)$.

Using the fact that the chain rule applies to matrix multiplications differentiating equation (1) with respect to time yields

$$\dot{\vec r}_I(t) = \mathbf T(t)\, \dot{\vec r}_F(t) + \dot{\mathbf T}(t)\, \vec r_F(t)\tag 2$$

So what is $\dot{\mathbf T}(t)$? The answer to this rhetorical question is that it can be expressed as the product of the matrix $\mathbf T(t)$ and a skew symmetric matrix which I'll call $\mathbf{Sk}_{\omega}(t)$. Proving this is nontrivial. See Time Derivative of Rotation Matrices: A Tutorial, for example, for a derivation. (The author of that paper uses $[\omega_B]_{\times}$ for what I'm calling $\text{Sk}_{\omega}(t)$; this is equation (3) in the linked paper.) Rewriting equation my equation (2) using this yields $$\dot{\vec r}_I(t) = \mathbf T(t)\, \dot{\vec r}_F(t) + \bigl(\mathbf T(t)\,\text{Sk}_{\omega}(t)\bigr)\, \vec r_F(t))$$ Matrix multiplication is associative and distributes over matrix addition, so the above can be rewritten as $$\dot{\vec r}_I(t) = \mathbf T(t) \left( \dot{\vec r}_F(t) + \text{Sk}_{\omega}(t)\, \vec r_F(t)\right)\tag 3$$ In three dimensional space (and only in three dimensional space), the product of a 3x3 skew symmetric matrix and a vector $\vec x$ can be expressed in terms of the cross product of a vector corresponding to the skew symmetric matrix (I'll call this $\vec\omega$) and the vector $\vec x$, and thus equation (3) becomes $$\dot{\vec r}_I(t) = \mathbf T(t) \left( \dot{\vec r}_F(t) + \vec\omega \times \vec r_F(t)\right)\tag 4$$ Some call this the kinematic transport theorem. Applying this a second time to obtain second derivatives yields $$\ddot{\vec r}_I(t) = \mathbf T(t) \left( \ddot{\vec r}_F(t) + \dot{\vec\omega}(t) \times \vec r_F(t) + 2 \vec\omega(t) \times \dot{\vec r}_F(t) + \vec\omega(t)\times(\vec\omega(t)\times \vec r_F(t))\right) \tag 5$$ This includes the coriolis effect, the centrifugal acceleration, and one term that Marion omitted, the Euler acceleration that results when $\vec\omega$ is not constant with respect to time.