Limitations Of Work-Energy Theorem

Question

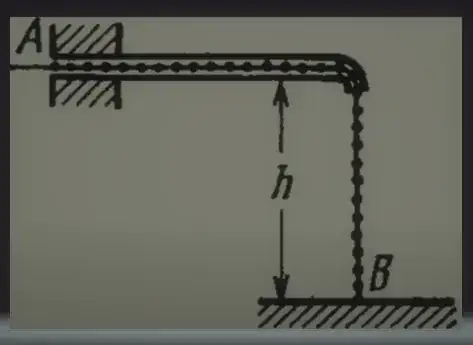
Consider the given system which shows a chain $AB$ of length $l$ and the end $A$ is held at rest.

Suppose we release the chain at time $t=0$. How do we find the velocity of the chain when the end $A$ is leaving the tube?

My approach was to use the work energy theorem. Let velocity of chain at time $t$ when it is leaving the tube be $v$. Also assume the chain has uniform mass distribution with linear mass density $\lambda$. $$W_{\textrm{gravity}}+W_{\textrm{normal}}=\Delta K=\frac{1}{2}(\lambda l)v^{2}$$ Work done by normal force can be taken as 0 as the point of application of force undergoes no displacement. $$W_{\textrm{gravity}}=\lambda(l-h)g\frac{h}{2}+\lambda(h)g\frac{h}{2}=\frac{\lambda ghl}{2}$$ This gives $v=\sqrt{gh}$ which is a contradictory result.

What is my mistake in the given argument and is there any discrepancy by writing the work-energy theorem (work done by net force as change in kinetic energy) here?

Answer 1

There are two issues here:

Work done by normal force can be taken as 0 as the point of application of force undergoes no displacement.

For the work-energy theorem the fact that the point of application of force undergoes no displacement is not relevant. Any force contributes to the net force and it is only the displacement of the center of mass that matters. So you cannot neglect the normal force here, and it is unknown. So the work-energy theorem will not help here.

The other issue is that your conservation of energy formula is incomplete. As the chain collides with the ground it loses KE and does not gain PE, so that lost KE goes to heat. In other words, the collision with the ground is inelastic. That lost energy must be accounted for when solving with energy.

Answer 2

According to me your answer is mostly correct, however, I would have considered that the chain undergoes circular motion in the very last bit of its motion. Hence,

$$ \frac {mv^2}{r} = mg\cos\theta $$ (considering v as the final velocity, and $r$ as the radius)

Hence, $$v=\sqrt {rg}\cos\theta$$

This is however my approach and I welcome any counter-opinions!