Viscoelastic Kelvin-Voigt model and inelastic strain

Question

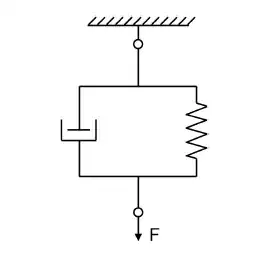
In a viscoelastic medium, the total strain can be assumed as the sum of elastic strain and inelastic strain (ref1,2):

\begin{align} \label{eq1} (1): \mathcal{E}^t_{ij}= \mathcal{E}^e_{ij}+\mathcal{E}^i_{ij} \end{align}

The inelastic strain is a kind of eigenstrain which is stress-free (ref3). So, the elastic stress (Cauchy stress) can then be derived linearly as: \begin{align} (2): \sigma^e= C_{ijkl}\mathcal{E}^e_{kl} \end{align}

However, one can simulate the the rheology by a Kelvin-Voigt model,

In this form, the elastic strain is equal to the viscous strain, does this contradict equation (1)? Is there any difference between the inelastic strain in equation (1) and the viscous strain in the Kelvin-Voigt mode?

Besides, if we want to calculate the effective viscosity (stress divided by strain rate), we may only use the inelastic strain rate of the system (excluding the elastic strain rate), but for the stress, should we use the elastic stress or total stress or the stress only related to the inelastic strain in the Kelvin-Voigt model? Or, in real material, the elastic stress is the total stress and there isn't any 'inelastic stress'?

ref1. Andrews, D. J. (1978). Coupling of energy between tectonic processes and earthquakes. Journal of Geophysical Research: Solid Earth, 83(B5), 2259-2264.

ref2. Barbot, S., & Fialko, Y. (2010). A unified continuum representation of post-seismic relaxation mechanisms: semi-analytic models of afterslip, poroelastic rebound and viscoelastic flow. Geophysical Journal International, 182(3), 1124-1140.

ref3. https://en.wikipedia.org/wiki/Eigenstrain

Answer 1

In this form, the elastic strain is equal to the viscous strain, does this contradict equation (1)? Is there any difference between the inelastic strain in equation (1) and the viscous strain in the Kelvin-Voigt mode?

My answer is valid for metals, but maybe it helps understanding a more general situation.

In an uniaxial test of the material, there are an elastic and a plastic region. The strain rate is an input (as temperature). For the same material and other set of conditions, we have a curve for each strain rate.

Supposing no unloading, the inclination of the curves in the plastic region (called strain hardening) can be associated with the elastic constant of a spring, and the sensibility of the material to the strain rate can be associated with a kind of damper.

For a given total strain, (and a strain rate) there is a stress. That is the yield stress for this condition. Let's call it $\sigma_e$

Now, back to 3D solid, we multiply the total strain tensor $\boldsymbol \epsilon_t$ by the elasticity tensor $\mathbf E$. If we are in the plastic region (at least for part of the solid), the components of the correspondent stress tensor $\boldsymbol \sigma$, when fed in the Von Mises formula, will result in a value above $\sigma_e$.

It is possible in finite element analysis to use an interative method to find a $\boldsymbol \epsilon$ that multiplied by $\mathbf E$ results finally in a $\boldsymbol \sigma$ that satisfies Von Mises criteria.

That strain tensor, because satisfies the elastic tensor relation, is the elastic strain tensor $\boldsymbol \epsilon_e$. The difference from the original strain tensor is the plastic tensor: $\boldsymbol \epsilon_p = \boldsymbol \epsilon_t - \boldsymbol \epsilon_e$

Answer 2

In this type of litterature, elastic strain means "strain that can be recovered after unloading" meaning that your material goes back to zero strain under zero stress either instantaneously (pure elastic behaviour) of after some time (viscoelastic behaviour). In this sense the K-V model only predicts elastic strains. This is different from inelastic strains due to plasticity in metal, crack opening in composite materials, etc... which will result in a residual strain after unloading.