2

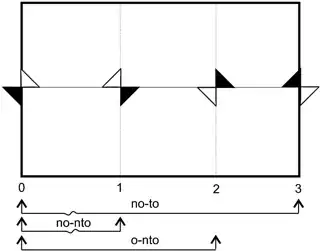
In the context of Lorentzian manifolds, we can define time orientability and space orientability as follows:

Time orientability: A Lorentzian manifold $(M,g_{ab})$ is time orientable if and only if there exists a continuous non-vanishing timelike vector field on $M$.

Space orientability: A Lorentzian manifold $(M,g_{ab})$ is space orientable if and only if there exists a continuous non-vanishing field of orthonormal triads of spacelike vectors on $M$.

My question is: are these two notions independent of one another? It's easy to think of cases where one property is messed up (e.g. by discontinuously turning the light cones), but then it seems that the other property is also messed up.

Jimeree
  • 233

2 Answers2

5

Yes, they are independent of each other.

  • For an example that is time-orientable but not space-orientable, start with $\mathbb{R}^4$ with the metric $dt^2-(dx^2+dy^2+dz^2)$ and then twist it by identifying $(t,-x,y,z)$ with $(t+1,x,y,z)$. This is still time-orientable (the vector field $\partial/\partial t$ is nonzero and timelike everywhere), but it's not orientable overall, so it can't be space-orientable.

  • For an example that is space-orientable but not time-orientable, start with $\mathbb{R}^4$ with the metric $dt^2-(dx^2+dy^2+dz^2)$ and then twist it by identifying $(-t,x,y,z)$ with $(t,x+1,y,z)$. This is still space-orientable (use the vector fields $\partial/\partial x$, $\partial/\partial y$, and $\partial/\partial z$ to see this), but it's not orientable overall, so it can't be time-orientable.

To see that time- and space-orientability together would imply overall orientability, just note that timelike and spacelike vector fields are necessarily linearly independent of each other everywhere. So, if the manifold admits a timelike vector field and three everywhere-linearly-independent spacelike vector fields, then it admits four everywhere-linearly-independent vector fields. Hence it admits an everywhere nonzero four-form, which implies (or is the definition of) overall orientability.

Related: Orientability of spacetime

Chiral Anomaly
  • 55,710
  • 5
  • 99
  • 166
1

To complement the other answer, see this paper:

Example 1.9 (A non-time orientable Lorentzian manifold) Consider $\mathbb{R}^2$ with Cartesian coordinates $(x, y)$ and metric $g = −\alpha \otimes \beta, \alpha = \cos \theta \,\mathrm{d}x + \sin \theta \,\mathrm{d}y, \beta = −\sin \theta \,\mathrm{d}x + \cos \theta \,\mathrm{d}y, \theta = \pi x/2$.

Then $M = [0,1] \times (−1,1)$ where the segment $\{0\} \times (−1,1)$ is glued to the segment $\{1\}×(−1,1)$ with a twist (see Fig. 1), and where the metric is the induced one provides the example we were looking for. This example is really non-orientable. To get an orientable example, glue $\{0\} \times (−1,1)$ to $\{2\} \times (−1,1)$ without a twist.

enter image description here

Fig. 1 Examples of non-orientable (no) or non-time orientable (nto) 2-dimensional Lorentzian manifolds. The curly line indicates that the edges have to be twisted and identified. The future cone is the white one

References:

  1. Lorentzian causality theory. Ettore Minguzzi. Living Reviews in Relativity, 22, 3. 2019-06-03.
user76284
  • 1,408